Число Маха — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 апреля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 апреля 2019; проверки требует 1 правка. У этого термина существуют и другие значения, см. Мах.Число́ Ма́ха (M{\displaystyle {\mathsf {M}}}) — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени немецкого учёного Эрнста Маха (нем. E. Mach).
Название число Маха и обозначение М предложил в 1929 году[1]Якоб Аккерет[2]. Ранее в литературе встречалось название число Берстоу[1][3] (Bairstow
Число Маха
- M=va,{\displaystyle {\mathsf {M}}={\frac {v}{a}},}
где v{\displaystyle v} — скорость потока, а a{\displaystyle a} — местная скорость звука,
является мерой влияния сжимаемости среды в потоке данной скорости на его поведение: из уравнения состояния идеального газа следует, что относительное изменение плотности (при постоянной температуре) пропорционально изменению давления:
- dρρ∼dpp,{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {dp}{p}},}
из закона Бернулли разность давлений в потоке dp∼ρv2{\displaystyle dp\sim \rho v^{2}}, то есть относительное изменение плотности:
- dρρ∼dpp∼ρv2p.{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {dp}{p}}\sim {\frac {\rho v^{2}}{p}}.}
Поскольку скорость звука a∼p/ρ{\displaystyle a\sim {\sqrt {p/\rho }}}, то относительное изменение плотности в газовом потоке пропорционально квадрату числа Маха:
- dρρ∼v2a2=M2.{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {v^{2}}{a^{2}}}={\mathsf {M}}^{2}.}
Наряду с числом Маха используются и другие характеристики безразмерной скорости течения газа:
коэффициент скорости
- λ=vvK=γ+12M(1+γ−12M2)−1/2{\displaystyle \lambda ={\frac {v}{v_{K}}}={\sqrt {\frac {\gamma +1}{2}}}{\mathsf {M}}\left(1+{\frac {\gamma -1}{2}}{\mathsf {M}}^{2}\right)^{-1/2}}
и безразмерная скорость
- Λ=vvmax=γ−12M(1+γ−12M2)−1/2,{\displaystyle \Lambda ={\frac {v}{v_{\max }}}={\sqrt {\frac {\gamma -1}{2}}}{\mathsf {M}}\left(1+{\frac {\gamma -1}{2}}{\mathsf {M}}^{2}\right)^{-1/2},}
где vK{\displaystyle v_{K}} — критическая скорость,
- vmax{\displaystyle v_{\max }} — максимальная скорость в газе,
- γ=cpcv{\displaystyle \gamma ={\frac {c_{p}}{c_{v}}}} — показатель адиабаты газа, равный отношению удельных теплоёмкостей газа при постоянных давлении и объёме соответственно.
Важное значение числа Маха объясняется тем, что оно определяет, превышает ли скорость течения газовой среды (или движения в газе тела) скорость звука или нет. Сверхзвуковые и дозвуковые режимы движения имеют принципиальные различия; для авиации это различие выражается в том, что при сверхзвуковых режимах возникают узкие слои быстрого значительного изменения параметров течения (ударные волны), приводящие к росту сопротивления тел при движении, концентрации тепловых потоков у их поверхности и возможности прогорания корпуса тел и тому подобное.
Предельно упрощённое объяснение числа Маха[править | править код]
Для понимания числа Маха неспециалистами очень упрощённо можно сказать, что численное выражение числа Маха зависит, прежде всего, от высоты полёта (чем больше высота, тем ниже скорость звука и выше число Маха). Число Маха — это истинная скорость в потоке вещества (то есть скорость, с которой воздух обтекает, например, самолёт), делённая на скорость звука в этом веществе в этих условиях. У земли скорость, при которой число Маха будет равно 1, будет равна приблизительно 340 м/с (скорость, с использованием которой люди оценивают расстояние до приближающейся грозы, измеряя время от вспышки молнии до дошедших раскатов грома) или 1224 км/ч. На высоте 11 км из-за падения температуры скорость звука ниже — около 295 м/с или 1062 км/ч.
Такое объяснение не может использоваться для каких бы то ни было математических расчётов скорости или иных математических операций по аэродинамике.
- ↑ 1 2 Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — С. 53. — 424 с. — ISBN 5–02–013814–2.
- ↑ Карман Т. Аэродинамика. Избранные темы в их историческом развитии / Под ред. А. В. Борисова. — М. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 111. — 208 с. — ISBN 5–93972–094–3.
- ↑ Гудымчук В. Подобие тепловое // Гл. ред. П. Н. Беликов Физический словарь. — М.: ОНТИ НКТП СССР, 1938. — Т. 4. — С. (столбцы) 228–229.
- ↑ Мхитарян А. М. Аэродинамика. — М., 1970. — С. 25. — 446 с. Переиздание: . — М.: Эколит, 2012. — ISBN 978–5–4365–0050–8.
- ↑ Аржанников Н. С., Мальцев В. Н. Аэродинамика. — М., 1956. — С. 314. — 484 с. Переиздание: . — М.: Эколит, 2011. — ISBN 978–5–4365–0030–0.
- Число Маха // Физическая энциклопедия. — М.: Советская энциклопедия, 1988.
- ГОСТ 25431-82 Таблица динамических давлений и температур торможения воздуха в зависимости от числа Маха
Число Маха — это… Что такое Число Маха?
У этого термина существуют и другие значения, см. Мах.Число́ Ма́ха () — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени австрийского учёного Эрнста Маха (нем. E. Mach).
Историческая справка
Название число Маха и обозначение М предложил в 1929 г.[1] Якоб Аккерет[2] (J.Ackeret). Ранее в литературе встречалось название число Берстоу[1][3] (Bairstow, обозначение ), а в советской послевоенной научной литературе — название
Число Маха
где — скорость потока, а — местная скорость звука,
является мерой влияния сжимаемости среды в потоке данной скорости на его поведение: из уравнения состояния идеального газа следует, что относительное изменение плотности (при постоянной температуре) пропорционально изменению давления:
из закона Бернулли разность давлений в потоке , то есть относительное изменение плотности:
Поскольку скорость звука , то относительное изменение плотности в газовом потоке пропорционально квадрату числа Маха:
Наряду с числом Маха используются и другие характеристики безразмерной скорости течения газа:
коэффициент скорости
и безразмерная скорость
где — критическая скорость,
- — максимальная скорость в газе,
- — показатель адиабаты газа, равный отношению удельных теплоёмкостей газа при постоянных давлении и объёме соответственно.
Максимально упрощённое объяснение числа Маха
Для понимания числа Маха неспециалистами очень упрощённо можно сказать, что численное выражение числа Маха зависит, прежде всего, от высоты полёта (чем больше высота и, соответственно, разрежение, тем ниже скорость звука и выше число Маха). Число Маха — это истинная скорость в потоке (то есть скорость, с которой воздух обтекает, например, самолёт), делённая на скорость звука в конкретной среде, поэтому зависимость является обратно пропорциональной. При давлении в 1 атм (у земли на уровне моря) скорость, соответствующая 1 Маху, будет равна приблизительно 300 м/с или 1100 км/ч, то есть скорости звука в воздухе. Однако, если, например, приборы самолёта показывают истинную скорость самолёта 1070 км/ч на высоте 11000 м, такой самолёт движется со скоростью более 1 Маха, то есть со сверхзвуковой скоростью.
Такое объяснение не может использоваться для каких бы то ни было математических расчётов скорости или иных математических операций по аэродинамике.
См. также
Литература
- Число Маха // Физическая энциклопедия. — М.: Советская энциклопедия, 1988.
Примечания
- ↑ 1 2 Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — С. 53. — 424 с. — ISBN 5–02–013814–2
- ↑ Карман Т. Аэродинамика. Избранные темы в их историческом развитии / Под ред. А. В. Борисова. — М.–Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 111. — 208 с. — ISBN 5–93972–094–3
- ↑ Гудымчук В. Подобие тепловое // Гл. ред. П. Н. Беликов Физический словарь. — М.: ОНТИ НКТП СССР, 1938. — Т. 4. — С. (столбцы) 228–229.
- ↑ Мхитарян А. М. Аэродинамика. — М., 1970. — С. 25. — 446 с. Переиздание: . — М.: Эколит, 2012. — ISBN 978–5–4365–0050–8
- ↑ Аржанников Н. С., Мальцев В. Н. Аэродинамика. — М., 1956. — С. 314. — 484 с. Переиздание: . — М.: Эколит, 2011. — ISBN 978–5–4365–0030–0
Число Маха — Википедия. Что такое Число Маха
Число́ Ма́ха (M{\displaystyle {\mathsf {M}}}) — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени австрийского учёного Эрнста Маха (нем. E. Mach).
Историческая справка
Название число Маха и обозначение М предложил в 1929 году[1]Якоб Аккерет[2] (J.Ackeret). Ранее в литературе встречалось название число Берстоу[1][3] (Bairstow[en], обозначение Ba{\displaystyle {\mathsf {Ba}}}), а в советской послевоенной научной литературе и, в частности, в советских учебниках 1950-х годов — название число Маиевского[4] (число Маха — Маиевского
Число Маха
- M=va,{\displaystyle {\mathsf {M}}={\frac {v}{a}},}
где v{\displaystyle v} — скорость потока, а a{\displaystyle a} — местная скорость звука,
является мерой влияния сжимаемости среды в потоке данной скорости на его поведение: из уравнения состояния идеального газа следует, что относительное изменение плотности (при постоянной температуре) пропорционально изменению давления:
- dρρ∼dpp,{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {dp}{p}},}
из закона Бернулли разность давлений в потоке dp∼ρv2{\displaystyle dp\sim \rho v^{2}}, то есть относительное изменение плотности:
- dρρ∼dpp∼ρv2p.{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {dp}{p}}\sim {\frac {\rho v^{2}}{p}}.}
Поскольку скорость звука a∼p/ρ{\displaystyle a\sim {\sqrt {p/\rho }}}, то относительное изменение плотности в газовом потоке пропорционально квадрату числа Маха:
- dρρ∼v2a2=M2.{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {v^{2}}{a^{2}}}={\mathsf {M}}^{2}.}
Наряду с числом Маха используются и другие характеристики безразмерной скорости течения газа:
коэффициент скорости
- λ=vvK=γ+12M(1+γ−12M2)−1/2{\displaystyle \lambda ={\frac {v}{v_{K}}}={\sqrt {\frac {\gamma +1}{2}}}{\mathsf {M}}\left(1+{\frac {\gamma -1}{2}}{\mathsf {M}}^{2}\right)^{-1/2}}
и безразмерная скорость
- Λ=vvmax=γ−12M(1+γ−12M2)−1/2,{\displaystyle \Lambda ={\frac {v}{v_{\max }}}={\sqrt {\frac {\gamma -1}{2}}}{\mathsf {M}}\left(1+{\frac {\gamma -1}{2}}{\mathsf {M}}^{2}\right)^{-1/2},}
где vK{\displaystyle v_{K}} — критическая скорость,
- vmax{\displaystyle v_{\max }} — максимальная скорость в газе,
- γ=cpcv{\displaystyle \gamma ={\frac {c_{p}}{c_{v}}}} — показатель адиабаты газа, равный отношению удельных теплоёмкостей газа при постоянных давлении и объёме соответственно.
Важность значения числа Маха
Важное значение числа Маха объясняется тем, что оно определяет, превышает ли скорость течения газовой среды (или движения в газе тела) скорость звука или нет. Сверхзвуковые и дозвуковые режимы движения имеют принципиальные различия; для авиации это различие выражается в том, что при сверхзвуковых режимах возникают узкие слои быстрого значительного изменения параметров течения (ударные волны), приводящие к росту сопротивления тел при движении, концентрации тепловых потоков у их поверхности и возможности прогорания корпуса тел и тому подобное.
Предельно упрощённое объяснение числа Маха
Для понимания числа Маха неспециалистами очень упрощённо можно сказать, что численное выражение числа Маха зависит, прежде всего, от высоты полёта (чем больше высота, тем ниже скорость звука и выше число Маха). Число Маха — это истинная скорость в потоке (то есть скорость, с которой воздух обтекает, например, самолёт), делённая на скорость звука в конкретной среде, поэтому зависимость является обратно пропорциональной. У земли скорость, соответствующая 1 Маху, будет равна приблизительно 340 м/с (скорость, с использованием которой люди оценивают расстояние до приближающейся грозы, измеряя время от вспышки молнии до дошедших раскатов грома) или 1224 км/ч. На высоте 11 км из-за падения температуры скорость звука ниже — около 295 м/с или 1062 км/ч.
Такое объяснение не может использоваться для каких бы то ни было математических расчётов скорости или иных математических операций по аэродинамике.
См. также
Примечания
- ↑ 1 2 Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — С. 53. — 424 с. — ISBN 5–02–013814–2.
- ↑ Карман Т. Аэродинамика. Избранные темы в их историческом развитии / Под ред. А. В. Борисова. — М. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 111. — 208 с. — ISBN 5–93972–094–3.
- ↑ Гудымчук В. Подобие тепловое // Гл. ред. П. Н. Беликов Физический словарь. — М.: ОНТИ НКТП СССР, 1938. — Т. 4. — С. (столбцы) 228–229.
- ↑ Мхитарян А. М. Аэродинамика. — М., 1970. — С. 25. — 446 с. Переиздание: . — М.: Эколит, 2012. — ISBN 978–5–4365–0050–8.
- ↑ Аржанников Н. С., Мальцев В. Н. Аэродинамика. — М., 1956. — С. 314. — 484 с. Переиздание: . — М.: Эколит, 2011. — ISBN 978–5–4365–0030–0.
Литература
- Число Маха // Физическая энциклопедия. — М.: Советская энциклопедия, 1988.
- ГОСТ 25431-82 Таблица динамических давлений и температур торможения воздуха в зависимости от числа Маха
Ссылки
Число Маха Википедия
У этого термина существуют и другие значения, см. Мах. Самолёт FA-18 Hornet , движущийся с околозвуковой скоростью. Наблюдается эффект Прандтля — ГлоертаЧисло́ Ма́ха (M{\displaystyle {\mathsf {M}}}) — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени немецкого учёного Эрнста Маха (нем. E. Mach).
Содержание
- 1 Историческая справка
- 2 Число Маха в газовой динамике
- 3 Важность значения числа Маха
- 4 Предельно упрощённое объяснение числа Маха
- 5 Примечания
- 6 Литература
- 7 Ссылки
Историческая справка[ | ]
Название число Маха и обозначение М предложил в 1929 году[1]Якоб Аккерет[2]. Ранее в литературе встречалось название число Берстоу[1][3] (Bairstow[en], обозначение Ba{\displaystyle {\mathsf {Ba}}}), а в советской послевоенной научной литературе и, в частности, в советских учебниках 1950-х годов — название число Маиевского[4] (число Маха — Маиевского) по имени основателя русской научной школы баллистики, пользовавшегося этой величиной, вместе с этим обозначение M{\displaystyle {\mathsf {M}}} употребляется без специального названия[5].
Число Маха
- M=va,{\displaystyle {\mathsf {M}}={\frac {v}{a}},}
где v{\displaystyle v}
Маха число — это… Что такое Маха число?
 Ударная волна в воздухе при числе Маха ≈ M1. Существует распространённое заблуждение, что возникновение облака из-за эффекта Прандтля — Глоерта означает, что именно в этот момент самолёт преодолевает «звуковой барьер». Проявление этого эффекта зависит от соотношения между скоростью самолёта, влажностью воздуха и температурой последнего. Конденсация пара вызвана градиентом температуры в области ударной волны.
Ударная волна в воздухе при числе Маха ≈ M1. Существует распространённое заблуждение, что возникновение облака из-за эффекта Прандтля — Глоерта означает, что именно в этот момент самолёт преодолевает «звуковой барьер». Проявление этого эффекта зависит от соотношения между скоростью самолёта, влажностью воздуха и температурой последнего. Конденсация пара вызвана градиентом температуры в области ударной волны.Число́ Ма́ха — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени австрийского ученого Эрнста Маха (нем. E. Mach).
Техническое определение
Зачастую используется упрощённое определение числа Маха как отношения скорости тела, движущегося в газовой среде, к скорости звука в данной среде. Такое определение не вполне корректно, так как скорости потоков в окрестностях движущегося тела зависят от его формы.
Чаще всего такое определение используется в оценочных характеристиках летательных аппаратов: их скорость задаётся безразмерным числом в формате M n, где n-десятичное число. Например, скорость M 4 — обозначает что скорость летательного аппарата в 4 раза превышает скорость звука. Пересчёт такой скорости в линейную скорость затруднён, так как скорость звука в воздухе зависит от его плотности (и, соответственно, высоты полёта) и температуры. Вместе с тем шкала скоростей Маха широко применяется в авиации, так как аэродинамические свойства и условия обтекания летательных аппаратов при близких значениях числа Маха также близки.
Число Маха
 , где
, где  — скорость потока, а
— скорость потока, а  — скорость звука
— скорость звука
является мерой влияния сжимаемости среды в потоке данной скорости на его поведение: из уравнения состояния идеального газа следует, что относительное изменение плотности (при постоянной температуре) пропорционально изменению давления:
 ,
,
из закона Бернулли разность давлений в потоке 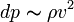 , то есть относительное изменение плотности:
, то есть относительное изменение плотности:
Поскольку скорость звука 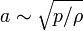 , то относительное изменение плотности в газовом потоке пропорционально квадрату числа Маха:
, то относительное изменение плотности в газовом потоке пропорционально квадрату числа Маха:
Наряду с числом Маха используются и другие характеристики безразмерной скорости течения газа:
коэффициент скорости
и безразмерная скорость
 ,
,
где 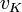 — критическая скорость,
— критическая скорость,
 — максимальная скорость в газе,
— максимальная скорость в газе, — отношение удельных теплоемкостей газа при постоянных давлении и объеме соответственно.
— отношение удельных теплоемкостей газа при постоянных давлении и объеме соответственно.
См. также
Литература
- Число Маха // Физическая энциклопедия, М: Советская энциклопедия, 1988
Wikimedia Foundation. 2010.
Число Маха — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Мах.Число́ Ма́ха (M{\displaystyle {\mathsf {M}}}) — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде — назван по имени австрийского учёного Эрнста Маха (нем. E. Mach).
Историческая справка
Название число Маха и обозначение М предложил в 1929 году[1]Якоб Аккерет[2] (J.Ackeret). Ранее в литературе встречалось название число Берстоу[1][3] (Bairstow[en], обозначение Ba{\displaystyle {\mathsf {Ba}}}), а в советской послевоенной научной литературе и, в частности, в советских учебниках 1950-х годов — название число Маиевского[4] (число Маха — Маиевского) по имени основателя русской научной школы баллистики, пользовавшегося этой величиной, вместе с этим обозначение M{\displaystyle {\mathsf {M}}} употребляется без специального названия[5].
Число Маха
- M=va,{\displaystyle {\mathsf {M}}={\frac {v}{a}},}
где v{\displaystyle v} — скорость потока, а a{\displaystyle a} — местная скорость звука,
является мерой влияния сжимаемости среды в потоке данной скорости на его поведение: из уравнения состояния идеального газа следует, что относительное изменение плотности (при постоянной температуре) пропорционально изменению давления:
- dρρ∼dpp,{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {dp}{p}},}
из закона Бернулли разность давлений в потоке dp∼ρv2{\displaystyle dp\sim \rho v^{2}}, то есть относительное изменение плотности:
- dρρ∼dpp∼ρv2p.{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {dp}{p}}\sim {\frac {\rho v^{2}}{p}}.}
Поскольку скорость звука a∼p/ρ{\displaystyle a\sim {\sqrt {p/\rho }}}, то относительное изменение плотности в газовом потоке пропорционально квадрату числа Маха:
- dρρ∼v2a2=M2.{\displaystyle {\frac {d\rho }{\rho }}\sim {\frac {v^{2}}{a^{2}}}={\mathsf {M}}^{2}.}
Наряду с числом Маха используются и другие характеристики безразмерной скорости течения газа:
коэффициент скорости
- λ=vvK=γ+12M(1+γ−12M2)−1/2{\displaystyle \lambda ={\frac {v}{v_{K}}}={\sqrt {\frac {\gamma +1}{2}}}{\mathsf {M}}\left(1+{\frac {\gamma -1}{2}}{\mathsf {M}}^{2}\right)^{-1/2}}
и безразмерная скорость
- Λ=vvmax=γ−12M(1+γ−12M2)−1/2,{\displaystyle \Lambda ={\frac {v}{v_{\max }}}={\sqrt {\frac {\gamma -1}{2}}}{\mathsf {M}}\left(1+{\frac {\gamma -1}{2}}{\mathsf {M}}^{2}\right)^{-1/2},}
где vK{\displaystyle v_{K}} — критическая скорость,
- vmax{\displaystyle v_{\max }} — максимальная скорость в газе,
- γ=cpcv{\displaystyle \gamma ={\frac {c_{p}}{c_{v}}}} — показатель адиабаты газа, равный отношению удельных теплоёмкостей газа при постоянных давлении и объёме соответственно.
Важность значения числа Маха
Важное значение числа Маха объясняется тем, что оно определяет, превышает ли скорость течения газовой среды (или движения в газе тела) скорость звука или нет. Сверхзвуковые и дозвуковые режимы движения имеют принципиальные различия; для авиации это различие выражается в том, что при сверхзвуковых режимах возникают узкие слои быстрого значительного изменения параметров течения (ударные волны), приводящие к росту сопротивления тел при движении, концентрации тепловых потоков у их поверхности и возможности прогорания корпуса тел и тому подобное.
Предельно упрощённое объяснение числа Маха
Для понимания числа Маха неспециалистами очень упрощённо можно сказать, что численное выражение числа Маха зависит, прежде всего, от высоты полёта (чем больше высота, тем ниже скорость звука и выше число Маха). Число Маха — это истинная скорость в потоке (то есть скорость, с которой воздух обтекает, например, самолёт), делённая на скорость звука в конкретной среде, поэтому зависимость является обратно пропорциональной. У земли скорость, соответствующая 1 Маху, будет равна приблизительно 340 м/с (скорость, с использованием которой люди оценивают расстояние до приближающейся грозы, измеряя время от вспышки молнии до дошедших раскатов грома) или 1224 км/ч. На высоте 11 км из-за падения температуры скорость звука ниже — около 295 м/с или 1062 км/ч.
Такое объяснение не может использоваться для каких бы то ни было математических расчётов скорости или иных математических операций по аэродинамике.
См. также
Примечания
- ↑ 1 2 Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — С. 53. — 424 с. — ISBN 5–02–013814–2.
- ↑ Карман Т. Аэродинамика. Избранные темы в их историческом развитии / Под ред. А. В. Борисова. — М. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 111. — 208 с. — ISBN 5–93972–094–3.
- ↑ Гудымчук В. Подобие тепловое // Гл. ред. П. Н. Беликов Физический словарь. — М.: ОНТИ НКТП СССР, 1938. — Т. 4. — С. (столбцы) 228–229.
- ↑ Мхитарян А. М. Аэродинамика. — М., 1970. — С. 25. — 446 с. Переиздание: . — М.: Эколит, 2012. — ISBN 978–5–4365–0050–8.
- ↑ Аржанников Н. С., Мальцев В. Н. Аэродинамика. — М., 1956. — С. 314. — 484 с. Переиздание: . — М.: Эколит, 2011. — ISBN 978–5–4365–0030–0.
Литература
- Число Маха // Физическая энциклопедия. — М.: Советская энциклопедия, 1988.
- ГОСТ 25431-82 Таблица динамических давлений и температур торможения воздуха в зависимости от числа Маха
Ссылки
Число Маха. (Сверхзвук, часть 2).
Здравствуйте, друзья!
Эрнст Мах. Идеалист с материалистическими наклонностями :-).
В сегодняшней небольшой статье немного пройдемся по теоретическим основам и коснемся одной из важнейших характеристик полета летательных аппаратов на большой скорости, в том числе и сверхзвуковой.
Сверхзвук и число Маха… Эти два понятия довольно тесно связаны и в наше время нет, наверное, ни одного человека, который бы так или иначе не слышал о числе М. Обычно этот термин сопровождает характеристики любого сверхзвукового (и даже просто скоростного) самолета. А самолетов таких у в мире сейчас немало и число их, я думаю, вряд ли будет уменьшаться :-).
Но ведь еще совсем не так давно теория сверхзвуковых течений была именно теорией, к тому же делающей, всего лишь, первые шаги. Фундаментальные основы она начала приобретать только около 140 лет назад, когда немецкий ученый и философ Эрнст Мах занялся исследованиями аэродинамических процессов при сверхзвуковом движении тел. В тот период он открыл и исследовал некоторые явления аэродинамики сверхзвука, получившие впоследствии свое название в его честь. В их ряду стоит и число Маха.
Интересен тот факт, что в советской науке (и в научной литературе, в особенности до войны и сразу после нее) этот термин часто употреблялся либо без расшифровки (просто число М, слово «Мах» не употеблялось), либо с использованием второй фамилии — Маиевский. То есть число Маха-Маиевского.
Все это было следствием нашего тогдашнего идеологического состояния. Эрнст Мах по своим философским взглядам (он был, по словам В.И.Ленина «субъективным идеалистом») не очень-то вписывался в рамки марксистско-ленинской философии, а Н.В.Маиевский был русским ученым, который занимался, в частности, проблемами внешней баллистики.
Внешняя баллистика — наука, исследующая движение тел после их выхода из устройства, придавшего им это движение, то есть, например, полет снаряда после его выхода из ствола артиллерийского орудия. Снаряд при этом летит с очень большой скоростью, в том числе и сверхзвуковой.
Вполне закономерно, что Н.В.Маиевский в своих исследованиях и разработках (передовых для своего времени и ставших впоследствии фундаментальными) оперировал понятием, аналогичным числу Маха, причем лет на 15 раньше своего немецкого коллеги.
А самое главное (для официальной идеологии :-)) было то, что русский ученый не был философом 🙂 и не имел взглядов, противоречащих марксистско-ленинской науке 🙂 …
Однако, как бы то ни было, сегодня едва ли не самое главное определение для сверхзвука носит имя (точнее фамилию :-)) немца Эрнста Маха. И само по себе это слово уже давно перестало быть просто фамилией. Мах, он мах и есть 🙂 . Только скорость, только полет 🙂 …
Вернемся, тем не менее, к конкретике. Что же такое это самое число М, и зачем оно вообще-то нужно в авиации? Ведь летали же себе люди раньше на дозвуковых скоростях безо всяких чисел Маха, да и сейчас подавляющее большинство летательных аппаратов на земле — дозвуковые. Однако, не все так просто, как выглядит :-).
При любом полете аппарата тяжелее воздуха одним из самых важных его параметров является скорость. Способов измерения скорости на сегодняшний день, вобщем-то, предостаточно :-). Для примера, параметры движения самолета относительно воздушной среды можно измерить следующими способами: ультразвуковой, термодинамический, тепловой, турбинный, манометрический.
А путевую скорость (то есть скорость относительно земли) можно измерить допплеровским, корелляционным, радиационным способом, а также способом визирования земной поверхности.
Но самый, так сказать, простой и логичный, давно применяющийся, а поэтому, естественно, проработанный и привычный все же аэрометрический (точнее говоря, аэродинамический) способ. С его помощью как раз и замеряется воздушная скорость самолета и число Маха.
Однако способ этот имеет определенные недостатки. Сам принцип его достаточно прост, и о нем мы уже ранее говорили. Воздух, набегая на летательный аппарат, в результате своего движения обладает некоторой кинетической энергией или, попросту говоря, скоростным напором (ρV²/2).
Попадая в приемник воздушного давления (ПВД, или Трубку Пито) он тормозится, и его напор превращается в давление на мембрану стрелочного прибора-указателя. Чем быстрее летит самолет, тем больше скоростной напор, тем большую скорость показывает стрелка прибора. То есть, вроде бы, все как по нотам.
Но не тут-то было :-). Пока летательный аппарат летит не очень быстро ( примерно до 400 км/ч) и не слишком высоко (тысяч где-то до 2-ух, 3-х) все действительно разворачивается просто и закономерно. А далее ноты начинают врать :-)…
Воздух взаимодействует с аэродинамическими поверхностями самолета, определяя тем самым параметры его полета. А эти параметры зависят от параметров состояния воздуха, как газа, которые, конечно, зависят от условий, в которых находится данный объем газа.
Например, с высотой падают плотность и температура воздуха. А чем плотность ниже, тем меньше будет скоростной напор, с которым набегающий поток давит на мембрану указателя скорости.
То есть получается, что если прибор в кабине пилота показывает одинаковую скорость на высотах, к примеру, 2000 м и 10000 м ( приборная скорость), то на самом деле это означает, что самолет на 10000 м относительно воздуха (и земли, конечно, тоже :-)) движется значительно быстрее (истинная скорость). Все из-за того, что воздух на высоте разрежен.
Плюс еще такая, не совсем, мягко говоря, удобная для полета вещь, как сжимаемость. Воздух — это газ, и, как любой газ, его можно при определенных условиях сжать, тем самым меняя параметры его состояния. Такие условия появляются при обтекании аэродинамических поверхностей на достаточно больших скоростях полета (формально отсчет начинают от 400 км/ч).
Воздух перестает быть однородной, одинаковой во всех направлениях средой, каковой он считается (хоть и довольно приближенно) для малоскоростных летательных аппаратов. Создаются условия для возникновения так называемых скачков уплотнения, меняются скорости движения воздушного потока на различных участках аэродинамической поверхности (профиля крыла, например), происходит сдвиг точки приложения аэродинамических сил, то есть меняется сам характер обтекания и, в конечном итоге, параметры управляемости летательного аппарата. То есть говоря «умными» терминами теории сверхзвука :-), начинается волновой кризис.
Однако, о нем мы еще будем говорить в дальнейшем. А пока можно заметить, что все эти процессы зависят от параметров воздушной среды и технико-конструктивных свойств самого летательного аппарата.
Чтобы описать аэродинамические свойства самолета во взаимодействии со средой, одной скорости движения бывает недостаточно. Ведь ее измеренная величина, качественно сама зависящая от параметров этой среды, не всегда характеризует истинную картину обтекания (как в примере выше).
Здесь нужен такой критерий, который бы учитывал «в себе» параметры потока и, опираясь на который, можно было бы всегда правильно охарактеризовать аэродинамические свойства летательного аппарата вне зависимости от условий полета.
Говоря это, я как раз и имею в виду число М. И слово «критерий» употребляю не случайно. Дело в том, что число Маха – это, говоря языком физики, один из критериев подобия в газовой динамике.
Смысл этого слегка замысловатого названия на самом деле прост и заключается в том, что если две или более физические системы имеют однотипные критерии подобия, равные по величине, то это означает, что рассматриваемые системы подобны, то есть похожи или, говоря совсем упрощенно (:-)) одинаковы.
Однако, если приборные скорости на этих высотах одинаковы, то это вовсе не означает, что указанное взаимодействие тоже будет одинаковым, скорее как раз наоборот. То есть скорость не может быть критерием подобия, и эти две системы в такой ситуации вовсе не подобны.
Однако, если мы говорим о том, что самолет на различных высотах (и вообще в различных условиях) летит с одинаковым числом Маха, то вполне правомерно утверждать, что условия обтекания и аэродинамические свойства на этих высотах (в этих условиях) будут одинаковы.
Здесь обязательно стоит сказать, что это утверждение, несмотря на свою верность, опирается, однако, на немалые упрощения. Первое – это то, что число Маха, хоть и основной для нас критерий подобия в газодинамике, но не единственный. А второе исходит из определения самого числа М.
Эрнст Мах, проводя свои исследования, вряд ли задумывался о применении их результатов в авиации :-). Ее тогда попросту не было. Определение было чисто научным и физически точным. Число Маха – это безразмерная величина, равная отношению скорости потока в данной точке движущейся газовой среды к скорости звука в этой точке.
То есть
Число Маха величина безразмерная. В единицах скорости выразить его невозможно, и перевод его в линейную скорость нецелесообразен из-за непостоянства скорости звука. Скорость летательного аппарата, используя число М, можно выразить только качественно, то есть оценивая, во сколько раз скорость самолета больше, либо меньше скорости звука.
При этом формат записи значений может быть как с использованием знака равенства, так и без него. Например запись М3 (как и М=3) может означать, что скорость летательного аппарата превысила скорость звука в три раза.
Упрощения применительно к авиации состоят в том, что скорость потока заменена на скорость движения физического тела в газовой среде, то есть имеется в виду истинная скорость движения самолета. За скорость звука принимается скорость звука на высоте полета. При этом, однако, не учитывается, что поток возле тела сложной формы, коим летательный аппарат и является :-), может иметь самые различные значения вблизи различных участков поверхности этого тела.
Указатель числа М на приборной доске сверхзвукового «Конкорда» (правый нижний угол). Над ним указатель скорости.
Однако, несмотря на достаточную некорректность упрощений, концепция числа Маха нашла в авиации очень широкое применение. Причем не только на сверхзвуковых самолетах, для которых сведения о числе М, так сказать, жизненно необходимы :-), но и на многих дозвуковых современных самолетах.
Ведь скорости их, хоть и дозвуковые, достаточно велики. К тому же практические высоты полетов тоже немаленькие. Так как скорость звука с высотой ощутимо падает, то возникает целесообразность на больших высотах использовать при пилотировании число Маха.
Для этого есть, по крайней мере, две причины. Во-первых, из-за большой разницы приборной и истинной скоростей, о чем я упоминал выше (лишние погрешности, к тому же очень ощутимые, никому не нужны :-)), а, во-вторых, для возможности оценки приближения волнового кризиса.
Дело в том, что для каждого типа летательного аппарата его проявления имеют место при определенных значениях числа М. В связи с этим практически все современные лайнеры имеют полетные ограничения по числу Маха для обеспечения устойчивого управления. Пилот при управлении самолетом следит за тем, чтобы это ограничение не было превышено.
Указатель приборной скорости и числа М (в центре) на приборной доске самолета ЯК-42.
Указатель истинной воздушной скорости и числа М (в центре) на приборной доске Boeing-747.
Таким образом число М — это не скорость в чистом виде, но, тем не менее, важный параметр, позволяющий экипажу правильно оценивать условия полета и осуществлять безопасное и точное управление летательным аппаратом.
Для получения информации о числе Маха практически все современные скоростные самолеты имеют в кабине экипажа указатель числа М. В просторечии его иногда именуют махметром. В большинстве случаев он представляет собой стрелочный указатель по типу указателя скорости. Такие приборы могут выдавать либо только значения числа Маха, либо могут быть объединены (скомбинированы) с указателем скорости, истинной или приборной.
Указатель числа М.
Указатель скорости УС-1600.
Указатель истинной скорости и числа М УСИМ-И. Такого типа указатель стоит на самолете МИГ-25.
Указатель истинной скорости и числа М (слева вверху) на приборной доске сверхзвукового МИГ-25.
Часто указатели числа М выполняют со специальным сигнализатором, который в нужный момент выдает предупреждение экипажу о превышении какого-либо порогового значения этого числа.
МС-1. Указатель числа М с электрической сигнализацией.
По своей конструкции и принципу действия указатель числа М вобщем-то аналогичен указателю воздушной (приборной ) скорости. Но для учета изменения условий с высотой в него добавлена анероидная коробка, реагирующая на изменение давления.
Кинематическая схема указателя числа М.
Подавляющее большинство современных самолетов летает все-таки на дозвуке. Этому режиму соответствует число Маха менее 0,8. Следующие режимы полета, на которых М принимает значения от 0,8 до 1,2 объединены под названием трансзвук. А когда число М меняется от 1,0 до 5,0, то это уже чистый сверхзвук, зона сверхзвукового полета современных военных самолетов.
Есть, правда, экземпляры напрямую к армии не относящиеся, более того достигающие скоростей, на которых число Маха превышает пять единиц. Это уже зона гиперзвука. Однако говорить об этих полуэкзотических аппаратах и режимах их полета мы будем уже в следующих статьях общей темы, посвященной сверхзвуку.
До новых встреч :-).
Фотографии кликабельны.
No related posts.

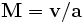 , где
, где 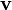 — скорость потока, а
— скорость потока, а 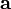 — скорость звука
— скорость звука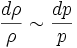 ,
,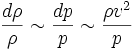
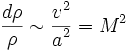
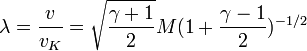
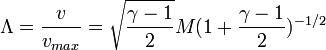 ,
,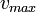 — максимальная скорость в газе,
— максимальная скорость в газе,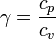 — отношение удельных теплоемкостей газа при постоянных давлении и объеме соответственно.
— отношение удельных теплоемкостей газа при постоянных давлении и объеме соответственно.