Дельты что такое: Значение слова ДЕЛЬТА. Что такое ДЕЛЬТА? – где находится, анатомия и функции дельт

Дельта — это… Что такое Дельта?

Дельта-4 — Дельта IV …   Википедия

Дельта IV — Старт РН Дельта IV Медиум со спутником DSCS III B6 Общие сведения …   Википедия

Дельта-2 — Дельта 2 …   Википедия

Дельта T — Дельта T, ΔT, Delta T, delta T, deltaT, или DT  обозначение временной разницы между земным временем (TT) и всемирным временем (UT). Содержание 1 Тонкости определения …   Википедия

ДЕЛЬТА — (греч.). Часть земли, находящаяся при устьях рек, между их рукавами; название это произошло оттого, что такой участок земли имеет обыкновенно форму греческой буквы дельты (?). Словарь иностранных слов, вошедших в состав русского языка. Чудинов… …   Словарь иностранных слов русского языка

дельта — 1. ДЕЛЬТА [дэ], ы; ж. Устье большой реки с его разветвлениями на отдельные рукава и прилегающая к нему суша. Д. Волги. ◁ Дельтовый, ая, ое. Д ые отложения. ● От названия греческой буквы, в начертании имеющей форму треугольника. 2. ДЕЛЬТА [дэ], ы; …   Энциклопедический словарь

ДЕЛЬТА — (греч. delta) 1) изменение цены опциона на будущую покупку или продажу акций, обусловленное изменением текущих цен акций. Обычно опцион на покупку имеет положительную Д., а опцион на продажу отрицательную. Это обусловлено тем, что если текущая… …   Юридическая энциклопедия

ДЕЛЬТА — [от названия заглавной буквы греческого алфавита А (дельта)], низменность в низовьях крупных рек, впадающих, как правило, в море. Область аккумуляции,где откладываются аллювиальные наносы. Если энергия реки велика, то благодаря наносам дельта… …   Экологический словарь

ДЕЛЬТА — ДЕЛЬТА, низменность в низовьях крупных рек, впадающих в мелководные участки моря или озера, образованная речными отложениями. Прорезана сетью рукавов и протоков. Название дельта происходит от заглавной буквы греческого алфавита D (дельта), по… …   Современная энциклопедия

ДЕЛЬТА — низменность в низовьях крупных рек, впадающих в мелководные участки моря или озера, образованная речными отложениями. Прорезана сетью рукавов и протоков. Название дельта происходит от заглавной буквы дельта греческого алфавита, по сходству с… …   Большой Энциклопедический словарь

ДЕЛЬТА — разветвление реки у ее устья на несколько рукавов, имеющее форму греческой буквы Δ (дельта). Образуется чаще в реках, впадающих во внутренние моря, где морские приливы слабы и не могут удалять из устья всех речных наносов; бывает также при… …   Морской словарь

дельта — Викисловарь

Морфологические и синтаксические свойства[править]

де́ль-та

Существительное, неодушевлённое, женский род, 1-е склонение (тип склонения 1a по классификации А. А. Зализняка).

Корень: -дельт-; окончание: -а.

Произношение[править]

• МФА: ед. ч. [ˈdɛlʲtə], мн. ч. [ˈdɛlʲtɨ]

Семантические свойства[править]

Значение[править]

1. четвёртая буква греческого алфавита (Δ, δ) ◆ Учитель подсел к ним, как к новичкам, и, увидев, что ни один из них не усвоил названий: альфа, вита, гамма, дельта и т. д., сокрушённо проговорил: — Ни знаись урок… Нихарасо, нихарасо! А. П. Чехов, «А. П. Чехов в греческой школе», 1907 г. (цитата из Национального корпуса русского языка, см. Список литературы)
2. геогр. низменность в низовьях реки, сложенная речными наносами и прорезанная разветвлённой сетью рукавов и протоков ◆ Стемнело, мы, ещё не выйдя в море, встали на якорь в дельте Северной Двины. Герард Васильев, «Роли, которые нас выбирают», 2002 г. (цитата из Национального корпуса русского языка, см. Список литературы)
3. матем. конечная разность при изменении какого-либо параметра ◆ Например, предположив, что скорость v частицы постоянна, можно определить её, если измерять расстояние дельта x, которое частица пройдёт за время дельта t… Л. Пономарев, «Атомы, лучи, кванты», 1969 г. // «Химия и жизнь» (цитата из Национального корпуса русского языка, см. Список литературы)

Синонимы[править]

1. —
2. —
3. частичн.: разность

Антонимы[править]

1. —
2. —
3. —

Гиперонимы[править]

1. буква
2. низменность, местность
3. разность, разница

Гипонимы[править]

1. —
2. —
3. —

Родственные слова[править]

Этимология[править]

Происходит от др.-греч. δέλτα «дельта», далее из финикийск. daleth «полог шатра».

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Анаграммы[править]

Библиография[править]

Морфологические и синтаксические свойства[править]

дель-та

Существительное, неодушевлённое, женский род.

Корень: -дельт-; окончание: -а.

Произношение[править]

Семантические свойства[править]

Значение[править]

1. четвёртая буква греческого алфавита (Δ, δ) ◆ Отсутствует пример употребления (см. рекомендации).
2. геогр. дельта (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).
3. матем. дельта (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы[править]

Антонимы[править]

Гиперонимы[править]

Гипонимы[править]

Родственные слова[править]

Ближайшее родство

Этимология[править]

Происходит от др.-греч. δέλτα «дельта», далее из финикийск. daleth «полог шатра».

Фразеологизмы и устойчивые сочетания[править]

Библиография[править]

Морфологические и синтаксические свойства[править]

дель-та

Существительное.

Корень: -дельт-; окончание: -а.

Произношение[править]

Семантические свойства[править]

Значение[править]

1. геогр. дельта (аналогично русскому слову) ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы[править]

Антонимы[править]

Гиперонимы[править]

Гипонимы[править]

Родственные слова[править]

Ближайшее родство

Этимология[править]

Происходит от др.-греч. δέλτα «дельта», далее из финикийск. daleth «полог шатра».

Фразеологизмы и устойчивые сочетания[править]

Библиография[править]

Дельта-функция — Википедия

Схематический график одномерной дельта-функции.

Де́льта-фу́нкция (или δ-функция, δ-функция Дирака, дираковская дельта, единичная импульсная функция

) — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенных или приложенных в одной точке.

Например, плотность единичной точечной массы m, находящейся в точке a одномерного евклидова пространства R1,{\displaystyle \mathbb {R} ^{1},} записывается с помощью δ{\displaystyle \delta }-функции в виде mδ(x−a).{\displaystyle m\delta (x-a).} Дельта-функция также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.

Несмотря на распространённую форму записи δ(x),x∈R,{\displaystyle \delta (x),x\in \mathbb {R} ,} δ{\displaystyle \delta }-функция не является функцией вещественной переменной, а определяется как обобщённая функция: непрерывный линейный функционал на пространстве дифференцируемых функций. Можно ввести производную для δ-функции, которая тоже будет обобщённой функцией, и интеграл, определяемый как функция Хевисайда. Нетрудно указать последовательности обычных классических функций, слабо сходящиеся к δ{\displaystyle \delta }-функции.

Можно различать одномерную и многомерные дельта-функции, однако последние могут быть представлены в виде произведения одномерных функций в количестве, равном размерности пространства, на котором определена многомерная функция.

Введена английским физиком Полем Дираком.

Существуют различные взгляды на понятие дельта-функции. Получающиеся при этом объекты, строго говоря, различны, однако обладают рядом общих характерных свойств. Все указанные ниже конструкции естественно обобщаются на случаи пространств большей размерности (Rn, n>1){\displaystyle (\mathbb {R} ^{n},\ n>1)}.

Простое определение[править | править код]

Дельта-функцию (функция Дирака) одной вещественной переменной можно определить как функцию δ(x){\displaystyle \delta (x)}, удовлетворяющую следующим условиям:

• δ(x)={+∞,x=0,0,x≠0;{\displaystyle \delta (x)=\left\{{\begin{matrix}+\infty ,&x=0,\\0,&x\neq 0;\\\end{matrix}}\right.}
• ∫−∞+∞δ(x)dx=1.{\displaystyle \int \limits _{-\infty }^{+\infty }\delta (x)\,dx=1.}

То есть эта функция не равна нулю только в точке x=0{\displaystyle x=0}, где она обращается в бесконечность таким образом, чтобы её интеграл по любой окрестности x=0{\displaystyle x=0} был равен 1. В этом смысле понятие дельта-функции аналогично физическим понятиям точечной массы или точечного заряда. Для понимания интеграла полезно представить себе некую фигуру на плоскости с единичной площадью, например, треугольник. Если уменьшать основание данного треугольника и увеличивать высоту так, чтобы площадь была неизменной, то в предельном случае мы получим треугольник с малым основанием и очень большой высотой. По предположению его площадь равна единице, что и показывает интеграл. Вместо треугольника можно без ограничения общности использовать любую фигуру. Аналогичные условия верны и для дельта-функций, определённых на Rn.{\displaystyle \mathbb {R} ^{n}.}

Эти равенства не принято считать определением дельта-функции, однако во многих учебниках по физике она определяется именно так, и этого достаточно для точного определения дельта-функции. Отметим, что из данного определения дельта-функции вытекает следующее равенство

∫−∞+∞δ(x−y)f(x)dx=f(y){\displaystyle \int \limits _{-\infty }^{+\infty }\delta (x-y)f(x)\,dx=f(y)}

(фильтрующее свойство) для любой функции f. Действительно, в силу свойства δ(x−y)=0{\displaystyle \delta (x-y)=0} при x≠y{\displaystyle x\neq y} значение этого интеграла не изменится, если функцию f(x){\displaystyle f(x)} заменить функцией f~(x){\displaystyle {\tilde {f}}(x)}, которая равна f(x){\displaystyle f(x)} в точке x=y{\displaystyle x=y}, а в остальных точках имеет произвольные значения. Например, берём f~(x)=f(y)=const{\displaystyle {\tilde {f}}(x)=f(y)=\operatorname {const} }, затем выносим f(y){\displaystyle f(y)} за знак интеграла и, используя второе условие в определении дельта-функции, получаем нужное равенство.

Производные от дельта-функции также почти всюду равны 0 и обращаются в ±∞{\displaystyle \pm \infty } при x=0{\displaystyle x=0}.

Классическое определение[править | править код]

Дельта-функция определяется как линейный непрерывный функционал на некотором функциональном пространстве (пространстве основных функций). В зависимости от цели и желаемых свойств, это может быть пространство функций с компактным носителем, пространство функций, быстро убывающих на бесконечности, гладких функций на многообразии, аналитических функций и т. д. Для того, чтобы были определены производные дельта-функции с хорошими свойствами, во всех случаях основные функции берутся бесконечно дифференцируемыми, пространство основных функций также должно быть полным метрическим пространством. Общий подход к обобщённым функциям см. в соответствующей статье. Такие обобщённые функции также называют распределениями.

Мы рассмотрим самый простой вариант. В качестве пространства основных функций рассмотрим пространство E{\displaystyle {\mathcal {E}}} всех бесконечно дифференцируемых функций на отрезке. Последовательность φn∈E{\displaystyle \varphi _{n}\in {\mathcal {E}}} сходится к φ∈E{\displaystyle \varphi \in {\mathcal {E}}}, если на любом компакте K∈R{\displaystyle K\in \mathbb {R} } функции φn{\displaystyle \varphi _{n}} сходятся к φ{\displaystyle \varphi } равномерно вместе со всеми своими производными:

limn→∞φn=φ⟺supjsupx∈K|φn(j)(x)−φ(j)(x)|→n→∞0.{\displaystyle \lim _{n\to \infty }\varphi _{n}=\varphi \iff \sup _{j}\sup _{x\in K}\left|\varphi _{n}^{(j)}(x)-\varphi ^{(j)}(x)\right|{\xrightarrow {n\to \infty }}\,0.}

Это локально выпуклое метризуемое пространство. Дельта-функцию определим как функционал δ∈E′{\displaystyle \delta \in {\mathcal {E}}^{\prime }}, такой что

∀φ∈E:⟨δ;φ⟩=φ(0).{\displaystyle \forall \varphi \in {\mathcal {E}}:\;\langle \delta ;\;\varphi \rangle =\varphi (0).}

Непрерывность означает, что если φn→φ{\displaystyle \varphi _{n}\to \varphi }, то ⟨δ;φn⟩→⟨δ;φ⟩{\displaystyle \langle \delta ;\;\varphi _{n}\rangle \to \langle \delta ;\;\varphi \rangle }. Здесь ⟨δ;φ⟩{\displaystyle \langle \delta ;\;\varphi \rangle } — значение функционала на функции φ{\displaystyle \varphi }.

Дельта-функция по Коломбо[править | править код]

Используемому для работы с дельта-функцией интегральному выражению можно придать смысл, близкий к интуитивному, в рамках теории алгебры обобщённых функций Коломбо (англ. Colombeau algebra) ^[1].

Пусть D{\displaystyle {\mathcal {D}}} — множество бесконечно дифференцируемых функций f:R→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} } с компактным носителем, то есть не равных нулю лишь на ограниченном множестве. Рассмотрим множество функций

A={φ∈D|∫Rφ(x)dx=1,∫Rxφ(x)dx=0}.{\displaystyle {\mathcal {A}}=\left\{\varphi \in {\mathcal {D}}\,{\bigg |}\int _{\mathbb {R} }\varphi (x)\,dx=1,\;\int _{\mathbb {R} }x\varphi (x)\,dx=0\right\}.}

Обобщённая функция — это класс эквивалентности функций R:A×R→R,{\displaystyle R\colon {\mathcal {A}}\times \mathbb {R} \to \mathbb {R} ,} R:(φ,x)↦R(φ,x),{\displaystyle R\colon (\varphi ,\;x)\mapsto R(\varphi ,\;x),} бесконечно дифференцируемых по x при каждом φ∈A{\displaystyle \varphi \in {\mathcal {A}}} и удовлетворяющих некоторому условию умеренности (полагая φε(x)=ε−1φ(xε−1),{\displaystyle \varphi _{\varepsilon }(x)=\varepsilon ^{-1}\varphi (x\varepsilon ^{-1}),} R(φε,x){\displaystyle R(\varphi _{\varepsilon },\;x)} и все её производные по x достаточно медленно растут при ε→0{\displaystyle \varepsilon \to 0}). Две функции полагаются эквивалентными, если R1−R2∈N{\displaystyle R_{1}-R_{2}\in {\mathcal {N}}}, где N{\displaystyle {\mathcal {N}}} — ещё один класс функций с ограничениями на рост R(φε,x){\displaystyle R(\varphi _{\varepsilon },\;x)} при ε→0.{\displaystyle \varepsilon \to 0.}

Дельта-функция определяется как δ(φ,x)=φ(−x).{\displaystyle \delta (\varphi ,\;x)=\varphi (-x).} Преимущество подхода Коломбо в том, что его обобщённые функции образуют коммутативную ассоциативную алгебру, при этом на множество обобщённых функций естественно продолжаются понятия интегрирования, дифференцирования, пределов, даже значения в точке. В этом смысле на дельта-функцию действительно можно смотреть как на функцию, равную 0 везде, кроме точки 0, и равную бесконечности в нуле, так как теория Коломбо включает в себя теорию бесконечно больших и бесконечно малых чисел, аналогично нестандартному анализу.

Подход Егорова[править | править код]

Аналогичная теория обобщённых функций была изложена в работе Ю. В. Егорова^[2]. Хотя она не эквивалентна теории Коломбо, конструкция значительно проще и обладает большинством желаемых свойств.

Обобщённая функция — это класс эквивалентности последовательностей f=(f1,f2,…),fi∈C∞(R).{\displaystyle f=(f_{1},\;f_{2},\;\ldots ),\;f_{i}\in C^{\infty }(\mathbb {R} ).} Последовательности f{\displaystyle f} и f~{\displaystyle {\tilde {f}}} считаются эквивалентными, если для любого компакта Ω⋐R{\displaystyle \Omega \Subset \mathbb {R} } функции последовательностей совпадают на Ω{\displaystyle \Omega } начиная с некоторого номера:

f∼f~⟺∀Ω⋐R ∃N ∀k>N:fk|Ω=f~k|Ω.{\displaystyle f\sim {\tilde {f}}\iff \forall \Omega \Subset \mathbb {R} \ \exists N\ \forall k>N\colon f_{k}|_{\Omega }={\tilde {f}}_{k}|_{\Omega }.}

Всевозможные операции над последовательностями (умножение, сложение, интегрирование, дифференцирование, композиция, …) определяются покомпонентно. Например, интеграл по множеству I определяется как класс эквивалентности последовательности

∫If(x)dx=[(a1,a2,…)],ai=∫Ifi(x)dx.{\displaystyle \int _{I}f(x)\,dx=[(a_{1},\;a_{2},\;\ldots )],\;a_{i}=\int _{I}f_{i}(x)\,dx.}

Две обобщённые функции слабо равны, если для любой бесконечно гладкой функции φ{\displaystyle \varphi }

limk→∞∫I(fk(x)−f~k(x))φ(x)dx=0.{\displaystyle \lim _{k\to \infty }\int _{I}(f_{k}(x)-{\tilde {f}}_{k}(x))\varphi (x)\,dx=0.}

При этом дельта-функция определяется любой дельта-образной последовательностью (см. ниже), все такие обобщённые функции слабо равны.

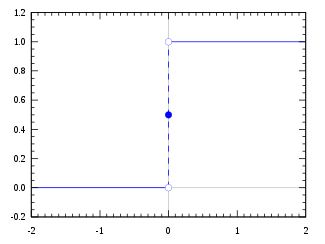Функция Хевисайда.

θ(x)={0,x<0,1,x>0.{\displaystyle \theta (x)=\left\{{\begin{array}{*{35}{l}}0,&x<0,\\1,&x>0.\\\end{array}}\right.}

• Фильтрующее свойство дельта-функции:

∫−∞+∞f(x)δ(x−x0)dx=f(x0).{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta (x-x_{0})\,dx=f(x_{0}).}

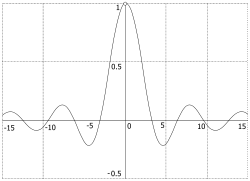График функции sin⁡xx.{\displaystyle {\frac {\sin x}{x}}.}

Пусть ∫−∞+∞f(x)dx=1.{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\,dx=1.}

Тогда последовательность

fn(x)=nf(nx){\displaystyle f_{n}(x)=nf(nx)}

слабо сходится к δ{\displaystyle \delta }-функции.

Выбор интегрируемой функции f(x),{\displaystyle f(x),} определённый интеграл которой в пределах от −∞{\displaystyle {-\infty }} до +∞{\displaystyle {+\infty }} равен 1 произволен.

Например, в качестве f(x){\displaystyle f(x)} можно выбрать функцию sinc: f(x)=sin⁡πxπx,{\displaystyle f(x)={\frac {\sin \pi x}{\pi x}},} дающую последовательность:

fn(x)=nsin⁡(nπx)nπx=sin⁡(nπx)πx.{\displaystyle f_{n}(x)=n{\frac {\sin(n\pi x)}{n\pi x}}={\frac {\sin(n\pi x)}{\pi x}}.}

При требовании, чтобы все функции в последовательности были всюду положительны, можно в качестве исходной функции выбрать, например, нормированную функцию Гаусса или иную любую всюду неотрицательную функцию, интеграл которой равен 1:

f(x)=1πe−x2,{\displaystyle f(x)={\frac {1}{\sqrt {\pi }}}e^{-x^{2}},}

fn(x)=nπe−(nx)2.{\displaystyle f_{n}(x)={\frac {n}{\sqrt {\pi }}}e^{-(nx)^{2}}.}

Во многих приложениях оказывается удобным интегральное представление дельта-функции:

δ(t)=12π∫−∞+∞eiωtdω.{\displaystyle \delta (t)={\frac {1}{2\pi }}\int \limits _{-\infty }^{+\infty }e^{i\omega t}\,d\omega .}

Доказательство

Рассмотрим интеграл

I(t)=12π∫−∞∞eiωtdω,{\displaystyle I(t)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }e^{i\omega t}\,d\omega ,}    (1)

который можно интерпретировать как предел

I(t)=limN→∞IN(t),{\displaystyle I(t)=\lim _{N\to \infty }I_{N}(t),}

где

IN(t)=12π∫−NNeiωtdω=1πNsin⁡tNtN.{\displaystyle I_{N}(t)={\frac {1}{2\pi }}\int \limits _{-N}^{N}e^{i\omega t}\,d\omega ={\frac {1}{\pi }}N{\frac {\sin {tN}}{tN}}.}    (2)

Известно, что

∫−∞∞sin⁡ttdt=π.{\displaystyle \int \limits _{-\infty }^{\infty }{\frac {\sin t}{t}}\,dt=\pi .}    (3)

В силу (3) для любого N{\displaystyle N} справедливо равенство:

∫−∞∞IN(t)dt=1π∫−∞∞sin⁡tNtNd(tN)=1.{\displaystyle \int \limits _{-\infty }^{\infty }I_{N}(t)\,dt={\frac {1}{\pi }}\int \limits _{-\infty }^{\infty }{\frac {\sin {tN}}{tN}}\,d(tN)=1.}    (4)

Можно показать (см. выше), что при неограниченном росте N для функции (2) оказываются верными все свойства дельта-функции и она в некотором смысле стремится к δ(t).{\displaystyle \delta (t).}

По определению производной дельта-функции δ(x){\displaystyle \delta (x)}:

∫−∞+∞f(x)δ′(x−a)dx=−f′(a){\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{\prime }(x-a)\,dx=-f^{\prime }(a)}

(распространение интегрирования по частям на случай подынтегральных выражений, содержащих дельта-функцию).

Аналогично для n-й производной дельта-функции:

∫−∞+∞f(x)δ[n](x−a)dx=−∫−∞+∞∂f∂xδ[n−1](x−a)dx.{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{[n]}(x-a)\,dx=-\int \limits _{-\infty }^{+\infty }{\frac {\partial f}{\partial x}}\delta ^{[n-1]}(x-a)\,dx.}

А проинтегрировав так по частям n раз, получим в конце концов:

∫−∞+∞f(x)δ[n](x−a)dx=(−1)n∂nf(x)∂xn|x=a.{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)\delta ^{[n]}(x-a)\,dx=\left.(-1)^{n}{\frac {\partial ^{n}f(x)}{\partial x^{n}}}\right|_{x=a}.}

Для производной дельта-функции имеет место тождество:

f(x)δ′(x)=f(0)δ′(x)−f′(0)δ(x),{\displaystyle f(x)\delta ^{\prime }(x)=f(0)\delta ^{\prime }(x)-f^{\prime }(0)\delta (x),}

которое можно получить дифференцируя произведение

Дельты — это… Что такое Дельты?

под этим названием разумели в древности трехугольные площади земной поверхности, напоминающие своей формой греческую букву Δ, расположенные в устье больших рек, преимущественно даже только Нила, и омываемые их рукавами, причем происхождение этих треугольных пространств вовсе не принималось в расчет. Современная геология ограничила, с одной стороны, это понятие, обозначая им лишь наносимые самой рекой и отлагаемые в устье образования, которые влекут за собой разделение реки на рукава, но, с другой стороны, и расширила понятие, разумея всякие наносные образования в устьях рек без различия формы их очертания, даже и такие, которые не успели еще подняться из-под уровня воды, но своим отложением заметно вызвали обмеление ближайшего к устью водного участка. Таким образом, из понятия Д. изъяты те напоминающие Д. образования, которые сложены не из наносной почвы, а из коренной породы и, следовательно, другого происхождения. Тут река, прокладывая русло, встречала значительное сопротивление со стороны подстилающей коренной породы, не могла достаточно углубить своего ложа и принуждена была разбиться на рукава, чтобы иметь возможность в то же время несколькими путями отводить притекающие воды. Лучшим примером для различия типичной Д. от дельтоподобных образований представляет Волга. В ее устье имеется настоящая Д., но на расстоянии 50 миль от устья она раздваивается на два рукава, соединяющихся во многих пунктах, оставляя между собой треугольное пространство. Это пространство, однако, не сложено из речных наносных отложений и не может назваться Д. Можно подразделить Д. на надводные и подводные. Последние суть не что иное, как зачаточные Д., переходящие со временем в настоящие надводные. Далее, по месту образования Д. можно подразделить на три категории: на пресноводные, образующиеся при устьях рек, впадающих или тоже в реку, или в озеро, морские и океанические — при устьях рек, впадающих в моря и океаны. Теория образования Д. зиждется на том факте, что с уменьшением скорости течения воды увеличивается количество отложения механически взвешенных в ней осадков. Река на всем своем протяжении, подмывая берега и размывая русло, уносит с собой значительное количество механически взвешенного материала: глину, песок, гальку и валуны. Количество этого материала зависит от скорости течения и от качества пород, слагающих русло и берега реки. Иногда это количество взвешенного материала бывает так велико, что от него зависит желтый и бурый цвет воды некоторых рек, как, напр., Роны до впадения в Женевское озеро и Зап. Двины. Если представить себе, что скорость течения реки при впадении ее в водный бассейн сразу уменьшится до нуля, то весь механически взвешенный материал станет осаждаться у самого устья и будет заполнять в данном месте постепенно глубину моря или озера. Сперва явится мель, которая постепенно образует низменные болотистые местности, заливаемые рекой в течение известной части года, причем вода, заливающая эти местности, осаждает, в свою очередь, новый приносимый материал. Д. начинает выступать иногда из-под поверхности, именно во время низкого стояния воды в реке, и река принуждена проложить себе русло уже в самой Д. Не будучи в состоянии смывать всего количества осадков, превышающих уровень ее русла, она расчленяется на ряд рукавов, прокладывающих себе самостоятельные русла. Но во время полноводия вся Д. все еще затопляется и увеличивается на всем пространстве, пока, наконец, не образуются на Д. высокие пункты, достигнуть кот. вода при наивысшем своем стоянии уже больше не может. Эти высокие участки становятся уже настоящей сушей, покрываются растительностью и заселяются животными, наконец и человеком. Иногда благодаря поднятиям Д. довольно быстро выводится из-под уровня бассейна. — Уменьшение скорости течения реки идет постепенно и влечет за собой сортировку осаждаемого материала по удельному весу. В ближайших участках от устья будут отлагаться наиболее тяжелые частицы, а затем, по мере удаления от устья, будут отлагаться все более и более легкие, а легчайшие глинистые частицы будут уноситься далеко и осядут, когда скорость течения станет приблизительно равной нулю. При этом комплекс тяжелых частиц образует более круто падающие слои, а песок и глина — пологие окраины Д. Эта сортировка материала наблюдается в старых Д. весьма наглядно. Но к этому материалу чисто минерального происхождения подмешиваются иногда илистые частицы, остатки растений и животных, которые продолжают разлагаться и обусловливают образование в некоторых Д. громадного количества газов. Напр., в Д. р. По из отверстий с силой исходят углеводородистые газы. Иногда выход газов сопровождается излиянием солевой воды, как это наблюдается в Д. р. Симето. — Мощность дельтовых осадков иногда превышает 100 м, как показали бурения в дельтах Нила, Миссисиппи, Роны и др. рек. — Форма и очертание Д. прежде всего находится в зависимости от контура берега бассейна, в который впадает река. Принимая во внимание ход образования Д., а priori можно сделать заключение, что она должна иметь форму треугольника, вершина которого обращена вверх по течению, но такая идеальная форма наблюдается сравнительно редко (напр. у Нила). Если берег моря или другого какого-нибудь бассейна при устье реки образует выпуклость, вдающуюся в водоем, то отложения Д. заполняют пространство перед выпуклостью и тем как бы увеличивают ее на счет бассейна; если же берег бассейна представляет прямую линию, то отложения Д. образуют ряд вдающихся выпуклостей. Примером такой выдающейся Д. может послужить дельта Лены. Она представляет собой неправильный треугольник, изрезанный сетью рукавов. Материковый берег крутой, а острова Д., образуемые рукавами, низменны и песчанисты. В случае же, если берег бассейна образует выгнутость, бухту, то отложения Д. будут заполнять ее и примут форму наиболее правильного треугольника. Такие Д. можно назвать выполняющими; они способствуют, в противоположность выдающимся, выпрямлению контуров берегов бассейнов. Пример подобной Д. представляет р. Нил. Между Ливийской пустыней, лежащей на плоскогорье в 150 метр. высоты, круто обрывающемся к морю, и Аравийской пустыней, расположенной приблизительно на такой же высоте, вдавалась некогда в форме клина бухта, которая ныне совершенно заполнена плодородным наносом Нила. Подобным же образом Нигер постепенно заполняет своими осадками Гвинейский залив и вызвал уже против своего устья довольно значительный мыс. Очевидно, что выполняющая Д. постепенно может перейти в выдающуюся. Заполнив совершенно бухту или залив, выпрямив контур берега в данном месте, река все будет продолжать отлагать свой механически взвешенный материал, который постепенно образует выдающуюся дельту; Д. р. Миссисипи может послужить тому подтверждением. Вся нижняя часть ее долины до реки Огио представляла собой в третичную геологическую эпоху, т. е. эпоху, предшествующую нашей, глубокий залив, который заполнен ныне третичными осадками, т. е. выполняющей дельтой Миссисипи. Когда, наконец, весь залив был выполнен, Д. Миссисипи стала выдвигаться и образовала уже в современную геологическую эпоху выдающуюся в Мексиканский залив Д. Имеют влияние на форму и очертания Д. также течения в бассейнах. Если перпендикулярно к течению реки идет, напр., морское течение, то осадки будут уноситься в сторону морского течения и образуют Д. в стороне от устья реки. У той же Миссисипи наблюдается подобное уклонение Д. в сторону. Именно в Мексиканском заливе проходит довольно сильное течение с З на В, поэтому и Д. Миссисипи отодвинута заметно на В.

Характер поверхности, величина и очертание Д. весьма различны. В общем поверхность всегда бывает совершенно горизонтальной и прорезана одним руслом реки или рядом ее рукавов, а форма — в виде неправильного треугольника. Очевидно, что та Д., которая образуется в тихом бассейне, будет иметь наипростейшую форму. В этом случае и русло реки будет проходить посередине ее, что наблюдается у р. Эбро. Но обыкновенно Д. подвергается затоплению как со стороны реки при половодье, так и со стороны бассейна, волнами которого постоянно размываются ближайшие ее участки. Что касается затопления рекой, то это ведет к образованию ряда рукавов, число, положение и направление которых подвержены постоянным изменениям. Напр., Урал некогда образовал при впадении в Каспийское море 19 рукавов, из которых теперь отводят воду лишь 5. Некоторые реки, как, напр., Лена, Нил, Дунай и др., образуют в своих Д. целую сеть рукавов. Д., образующиеся в тихих озерах, увеличиваются гораздо быстрее, чем, напр., морские или океанйческие; подверженные почти постоянному размыву волн. Озера, через которые протекают реки, служат для них очистительными бассейнами, удерживая их механические и химические примеси. Если такая очищенная река протекает по руслу, трудно поддающемуся размыву, то она и не содержит в своей воде механически взвешенного материала и не может образовать при устье своем Д., что и наблюдается в Швеции у рек, соединяющих ряд озер. Затем, если морской бассейн, в который впадает река, очень глубок, то речные осадки распределяются по дну, не образуя Д. Остановимся на Д. р. Невы. Одна Нева отводит в море воды Ладожского и Онежского озер. С высоты 5 метр. очищенная от механических примесей вода Ладожского озера, пройдя по Неве 67 км, достигает Финского залива. Материал от размыва по пути берегов образовал в устье Невы и образует поныне еще Д., т. е. острова и часть береговой полосы, на которых расположен С.-Петербург. Сохранившиеся съемки 1718, 1777 и 1864 гг. дают возможность до некоторой степени судить о годовом приросте Д. Невы и тем приблизительно определить ее древность.

—————————————————————————————————————————

|                                                        | С 1718 по 1777       | С 1777 по 1864        |

|————————————————————————————————————————|

| Прирост Петербургского о-ва          | 0,020                     | 0,038                      |

|————————————————————————————————————————|

| Прирост Каменного о-ва                  | 0,113                     | 0,125                      |

|————————————————————————————————————————|

| Прирост Елагина о-ва                      | 0,148                     | 0,188                      |

|————————————————————————————————————————|

| Прирост Васильевского о-ва           | 0,125                     | 0,148                      |

|————————————————————————————————————————|

| Прирост Гутуевского о-ва                | 0,469                     | 0,499                      |

—————————————————————————————————————————

Из этих цифр следует, что увеличиваются быстрее острова, обращенные к морю, и притом острова с меньшей площадью. Если допустить, что Нева равномерно (что, впрочем, было бы неточно) увеличивала свою Д., то время, необходимое для образования всех островов, будет по простому расчету 932 года; таков приблизительно возраст невской Д. Нужно заметить, что не весь механически взвешенный материал р. Невы идет на увеличение островов, большая часть его идет и на увеличение ближайших к устью участков сев. и юж. побережий Финского залива. Так, в 30 лет лахтинский (сев.) берег увеличился на 1127100 вв. м, а юж. на 1654100 кв. м; значит, в год увеличение обоих берегов равно 55103 кв. м. Увеличение как юж., так и сев. берегов на счет Финского залива наводит на мысль, что будет время, когда все пространство между устьем Невы и Кронштадтом будет заполнено дельтовыми осадками и Нева будет впадать в море у Кронштадта. Для этого необходимо более 3000 лет. Таким образом Д. р. Невы еще молодая, если сравнить ее с Д. р. Миссисипи, которая начала образовываться в предшествующую современной, т. е. третичную геологическую эпоху. Во все геологические эпохи существовали Д., но, разумеется, их нелегко реставрировать. Однако изучение геологического строения современных Д. дало возможность отнести во многих местах Англии береговую формацию каменноугольной системы к дельтовым образованиям. К таковым же образованиям причисляют ныне конгломератовые, богатые растительными и животными (раковины) остатками банки в песках меловой системе окрестностей г. Аахена.

Г. Петц.

Значение слова «Дельта» в 10 онлайн словарях Даль, Ожегов, Ефремова и др.

Поделиться значением слова:

ж. греч. земли, между расходяшимися устьями реки, образующие треугольник; межеустье.

ДЕЛЬТА [дэ], -ы, ж. Устье большой реки с его разветвлениями на отдельные рукава и прилегающая к нему часть суши. Д. Волги. || прил. дельтовый, -ая, -ое.

ДЕ́ЛЬТА дэ, дельты, ·жен.
1. Название четвертой буквы ·греч. алфавита (D).
2. Устье реки, разветвляющейся на отдельные рукава (геогр.). Дельта Волги.

низовье, буква, устье, авандельта, впадение

низменность в низовьях крупных рек, впадающих в мелководные участки моря или озера, образованная речными отложениями. Прорезана сетью рукавов и протоков. Название дельта происходит от заглавной буквы «дельта» греческого алфавита, по сходству с которой оно было дано в древности треугольной дельте Нила.

авандельта, буква, впадение, низовье, устье

де́льта,
де́льты,
де́льты,
де́льт,
де́льте,
де́льтам,
де́льту,
де́льты,
де́льтой,
де́льтою,
де́льтами,
де́льте,
де́льтах

{дэ}, ы, ж.

1. Четвертая буква греческого алфавита: D, d. | В специальных текстах д. используется в качестве символа для обозначения переменной величины.||Ср. АЛЬФА, БЕТА, ГАММА II, ЗЕТ, ИГРЕК, ИКС, ИПСИЛОН, ЛЯМБДА, НЮ II, ОМЕГА, СИГМА.

2. Устье реки с его разветвлениями на отдельные рукава и прилегающие к нему части суши (название дано по сходству с видом заглавной буквы D). Д. Волги. Дельтовый — относящийся к дельте, дельтам.||Ср. ЭСТУАРИЙ» title=’ЭСТУАРИЙ, ЭСТУАРИЙ это, что такое ЭСТУАРИЙ, ЭСТУАРИЙ толкование’>ЭСТУАРИЙ.

Поделиться значением слова:

Дельта — это… Что такое Дельта?

        сложенная речными наносами низменность в низовьях реки, прорезанная более или менее разветвлённой сетью рукавов и протоков. Название Д. происходит от заглавной буквы греческого алфавита Δ (дельта), по сходству с которой оно было дано в древности треугольной дельте р. Нил. Д. образуется в результате сложного взаимодействия речного стока, морского волнения, приливов и сгонно-нагонных течений. Формирование Д. в условиях мелководного взморья начинается с возникновения коротких приустьевых кос и подводных отмелей (осередков) в самом русле или отмелей (устьевых баров, «россыпей») на морском крае. Во время половодий осередки и приустьевые бары постепенно становятся надводными и превращаются в низменные острова, разделяющие русло на рукава. В условиях приглубого взморья волны строят из выносимого рекой материала береговые валы, окаймляющие морской край Д. Благоприятными условиями для быстрого роста Д. являются: обилие приносимых рекой наносов, в некоторых случаях понижение уровня водоёма (или тектоническое поднятие берега), положение устья в вершине залива или в лагуне (блокированные Д.), а также мелководность бассейна, куда впадает река. Препятствуют образованию Д. сильные приливо-отливные и сгонно-нагонные течения и быстрое повышение уровня водоёма (быстрое тектоническое погружение). Скорость нарастания Д. колеблется в широких пределах — от нескольких метров до сотен метров в год. Например, при стабильном стоянии уровня Каспийского моря (1863—1914) линейное нарастание дельты Волги составляло 94 м в год; за период 1930—40 — до 0,7—1 км в год.

         Растущие в вершинах заливов Д. носят название Д. заполнения (или выполнения), Д. открытого морского побережья — Д. выдвижения. По способу образования и по стадиям развития различают следующие типы Д.: клювообразные (Тибр), лопастные (Миссисипи), блокированные (Камчатка), выдвинутые, с открытым округлым морским краем (Нигер), многоостровные (Волга). При малом количестве наносов и при понижении уровня моря речные рукава врезаются в отложения, слагающие поверхность приустьевого участка суши (морские или иные по генезису), и образуются врезанные дельты (Нева).

         Д. крупных рек достигают больших размеров: площадь Д. Амазонки 100 тыс. км², Лены 28,5 тыс. км², Волги 19 тыс. км². Плодородие почв и увлажнённость определяют высокую ценность земель значительной части территории многих Д., являющихся районами интенсивного земледелия (например, Д. Нила, Хуанхэ, Ганга).

         Лит.: Самойлов И. В., Устья рек, М., 1952; Леонтьев О. К., Основы геоморфологии морских берегов и дна, М., 1961; Залогин Б. С., Родионов Н. А., Устьевые области рек СССР, М., 1969.

         О. К. Леонтьев.

        

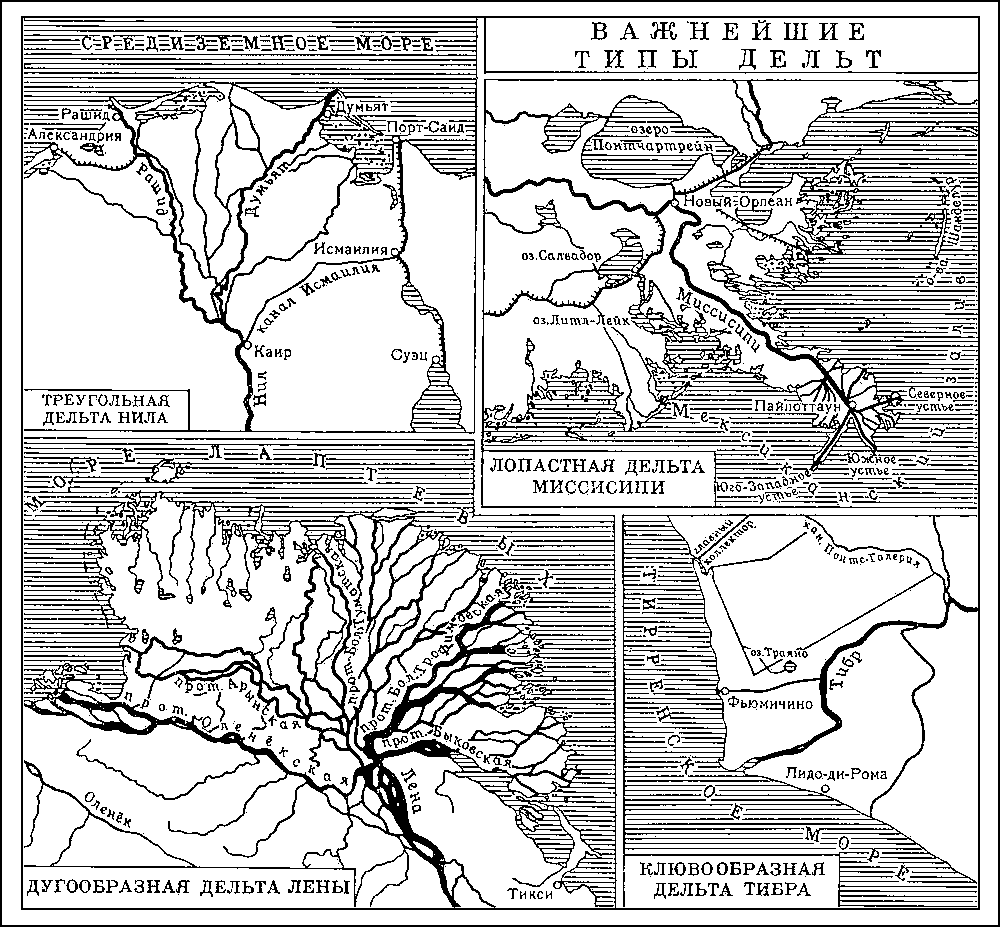
        Важнейшие типы дельт.

дельта — это… Что такое дельта?

Дельта-4 — Дельта IV …   Википедия

Дельта IV — Старт РН Дельта IV Медиум со спутником DSCS III B6 Общие сведения …   Википедия

Дельта-2 — Дельта 2 …   Википедия

Дельта T — Дельта T, ΔT, Delta T, delta T, deltaT, или DT  обозначение временной разницы между земным временем (TT) и всемирным временем (UT). Содержание 1 Тонкости определения …   Википедия

ДЕЛЬТА — (греч.). Часть земли, находящаяся при устьях рек, между их рукавами; название это произошло оттого, что такой участок земли имеет обыкновенно форму греческой буквы дельты (?). Словарь иностранных слов, вошедших в состав русского языка. Чудинов… …   Словарь иностранных слов русского языка

дельта — 1. ДЕЛЬТА [дэ], ы; ж. Устье большой реки с его разветвлениями на отдельные рукава и прилегающая к нему суша. Д. Волги. ◁ Дельтовый, ая, ое. Д ые отложения. ● От названия греческой буквы, в начертании имеющей форму треугольника. 2. ДЕЛЬТА [дэ], ы; …   Энциклопедический словарь

ДЕЛЬТА — (греч. delta) 1) изменение цены опциона на будущую покупку или продажу акций, обусловленное изменением текущих цен акций. Обычно опцион на покупку имеет положительную Д., а опцион на продажу отрицательную. Это обусловлено тем, что если текущая… …   Юридическая энциклопедия

ДЕЛЬТА — [от названия заглавной буквы греческого алфавита А (дельта)], низменность в низовьях крупных рек, впадающих, как правило, в море. Область аккумуляции,где откладываются аллювиальные наносы. Если энергия реки велика, то благодаря наносам дельта… …   Экологический словарь

ДЕЛЬТА — ДЕЛЬТА, низменность в низовьях крупных рек, впадающих в мелководные участки моря или озера, образованная речными отложениями. Прорезана сетью рукавов и протоков. Название дельта происходит от заглавной буквы греческого алфавита D (дельта), по… …   Современная энциклопедия

ДЕЛЬТА — низменность в низовьях крупных рек, впадающих в мелководные участки моря или озера, образованная речными отложениями. Прорезана сетью рукавов и протоков. Название дельта происходит от заглавной буквы дельта греческого алфавита, по сходству с… …   Большой Энциклопедический словарь

ДЕЛЬТА — разветвление реки у ее устья на несколько рукавов, имеющее форму греческой буквы Δ (дельта). Образуется чаще в реках, впадающих во внутренние моря, где морские приливы слабы и не могут удалять из устья всех речных наносов; бывает также при… …   Морской словарь