Виды дистанций и энергетика бега
Зачем солить воду и почему паста накануне забега — лучшая еда? Разбираемся с энергетикой бега.
Во время пробежки наш организм 👇
🔥🥓 Окисляет гликоген и жир. Бег на длинные дистанции — это в первую очередь аэробные нагрузки. Во время таких нагрузок работают красные мышечные волокна с активным участием сердечно-сосудистой системы. У нас поднимается пульс и учащается дыхание. А наш организм использует запасы гликогена в мышцах и жир, чтобы получить из них энергию с помощью кислорода. Так что похудеть с помощью пробежек вполне реально.
❗️ Хотя во время длинной пробежки организм активно расщепляет жир, он вряд ли закончится. Даже у невероятно худых ультрамарафонцев жира сохраняется не меньше 10%.
🥵💦 Теряет воду и электролиты. Пробежки нагревают наше тело — тепло выделяется при получении энергии. Чтобы охладить себя, мы потеем, а вместе с потом теряем воду и электролиты.
😍🍌 Плохо переваривает еду. Во время пробежки кровь приливает к работающим органам: мышцам и сердцу, а не к желудку. Так что бег после еды вполне может привести к несварению — есть плотно стоит за пару часов. Особенно не стоит есть жирную еду — она долго и сложно переваривается. Также не стоит есть овощи и фрукты: клетчатка тоже переваривается долго. Максимум, что можно съесть перед пробежкой — один апельсин или банан.
🍝🍣 Подготовка к забегу. Если на следующее утро вы планируете забег больше 10 км, лучше помочь организму и вечером поесть медленных углеводов: пасты, риса или картофеля. После расщепления энергия пойдет в запасы мышечного гликогена и наутро даст вам энергию на пробежке. А если забег будет длинным, то обычно на маршруте есть остановки с фруктами — не пробегайте мимо. Другой вариант — гели с электролитами и глюкозой. Они восполнят запасы энергии и помогут добежать до цели.
А если забег будет длинным, то обычно на маршруте есть остановки с фруктами — не пробегайте мимо. Другой вариант — гели с электролитами и глюкозой. Они восполнят запасы энергии и помогут добежать до цели.
Легкая атлетика. Виды дистанций
Первые Олимпийские игры древности, о которых сохранилась достоверная запись, состоялись в 776 г. до н.э. Тогда в программу состязаний входил лишь бег на 1 стадий (192 м 27 см).
Бег — на короткие (100, 200, 400 м), средние (800 и 1500 м), длинные (5000 и 10 000 м) и сверхдлинные дистанции (марафонский бег — 42 км 195 м), эстафетный бег (4 х 100 и 4 х 400 м), бег с барьерами (100 м — женщины, ПО м — мужчины, 400 м — мужчины и женщины) и бег с препятствиями (3000 м). Соревнования по бегу — один из самых старых видов спорта, по которым были утверждены официальные правила соревнований, и были включены в программу с самых первых олимпийских игр 1896 года. Для бегунов важнейшими качествами являются: способность поддерживать высокую скорость на дистанции, выносливость (для средних и длинных), скоростная выносливость (для длинного спринта), реакция и тактическое мышление.
Беговые виды входят как в состав дисциплин лёгкой атлетики, так и во многие популярные виды спорта отдельными этапами (в эстафетах, многоборьях). Соревнования по бегу проводятся на специальных легкоатлетических стадионах с оборудованными дорожками. На летних стадионах обычно 8-9 дорожек, на зимних 4-6 дорожек. Ширина дорожки — 1.22 м, линии, разделяющей дорожки — 5 см. На дорожки наносится специальная разметка указывающая старт и финиш всех дистанций, и коридоры для передачи эстафетной палочки. Сами соревнования почти не требуют сколько-нибудь особенных условий. Определённое значение имеет покрытие, из которого изготовлена беговая дорожка. Исторически сначала дорожки были земляными, гаревыми, асфальтовыми. В настоящее время дорожки на стадионах изготовлены из синтетических материалов.
Соревнования по бегу проводятся на специальных легкоатлетических стадионах с оборудованными дорожками. На летних стадионах обычно 8-9 дорожек, на зимних 4-6 дорожек. Ширина дорожки — 1.22 м, линии, разделяющей дорожки — 5 см. На дорожки наносится специальная разметка указывающая старт и финиш всех дистанций, и коридоры для передачи эстафетной палочки. Сами соревнования почти не требуют сколько-нибудь особенных условий. Определённое значение имеет покрытие, из которого изготовлена беговая дорожка. Исторически сначала дорожки были земляными, гаревыми, асфальтовыми. В настоящее время дорожки на стадионах изготовлены из синтетических материалов.
В качестве обуви спортсмены используют специальные беговые туфли — шиповки, обеспечивающие хорошее сцепление с покрытием. Соревнования по бегу проводятся практически в любую погоду. В жаркую погоду в беге на длинные дистанции могут также организовываться пункты питания. В ходе бега спортсмены не должны мешать друг другу, хотя при беге особенно на длинные и средние дистанции возможны контакты бегунов.
Бег на короткие дистанции (спринт) характеризуется выполнением кратковременной работы максимальной интенсивности. К нему относится бег на дистанции от 30 до 400 м. Для удобства изучения технику бега принято условно подразделять на четыре части: начало бега (старт), стартовый разбег, бег по дистанции и финиширование.
В беге на 200 и 400 м старт принимают обычно на вираже беговой дорожки. Это позволяет пробегать начальный отрезок дистанции по прямой: при этом легче развить максимальную скорость. При подбегании к повороту для борьбы с центробежными силами спринтер плавно наклоняет туловище влево и слегка поворачивает в эту же сторону стопы ног. Чем выше скорость бега и больше кривизна поворота дорожки, тем больше туловище наклоняется к центру окружности.
Чем выше скорость бега и больше кривизна поворота дорожки, тем больше туловище наклоняется к центру окружности.
Эстафетный бег — командный вид соревнований, в котором участники поочередно пробегают отрезки дистанции, передавая друг другу эстафетную палочку. По правилам соревнований эстафетная палочка имеет массу не менее 50г, длину 30 см и диаметр 4 см, Передача эстафетной палочки разрешается только в зоне, по длине равной 20 м. Техника бега с эстафетной палочкой практически не отличается от бега по дистанции. Важное значение в эстафетном беге имеет техника передачи эстафетной палочки, которая происходит на большой скорости в ограниченной зоне.
Команда считается закончившей дистанцию бега в том случае, если эстафетная палочка пронесена от старта до финиша без нарушений правил соревнований. Она передается из рук в руки, бросать ее или перекатывать по дорожке не разрешается. Если во время передачи эстафетная палочка будет обронена, то ее должен поднять передающий.
В беге на средние дистанции (500-2000 м) спортсмены обычно применяют высокий старт. По вызову судьи на старте бегуны выходят на линию сбора обычно в 3 м от линии старта. По команде «На старт!» они подходят к линии старта и занимают наиболее выгодное положение для начала бега. При этом бегун ставит у стартовой линии сильнейшую ногу, отставляя другую назад. Разноименная выставленной вперед ноге согнутая рука выносится вперед. Некоторые бегуны опираются этой рукой о землю (до стартовой линии). В беге на средние дистанции команда «Внимание!» не подается. По команде «Марш!» или выстрелу бегуны устремляются вперед.
Бег по пересеченной местности (кросс) — один из прикладных видов легкой атлетики. Бег в естественных условиях на местности укрепляет организм, положительно действует на нервную систему, является важным средством подготовки спортсменов многих видов спорта; они применяют бег по пересеченной местности в процессе своей тренировки.
Кросс является не только вспомогательным средством тренировки спортсменов, но и самостоятельным видом спортивного бега. Отличительной особенностью этого вида бега является значительная продолжительность и высокая интенсивность мышечной работы. Бег по пересеченной местности проводится по общей дорожке с высокого старта. Дистанцию кросса прокладывают по полям, лесам и оврагам. На них могут быть естественные и искусственные препятствия: рвы, канавы или изгороди не выше 1 м. При беге в лесу необходимо внимательно смотреть под ноги, а руками предохранять лицо, шею, плечи и туловище от ударов ветвей.
Стайерский бег: виды, дистанции, техника
Какие дистанции чаще всего берутся для организации любительских соревнований? Часто ли вы видите анонсы о проведении открытой для всех желающих гонки на 400 м либо на милю? Забеги от 5 км до марафона получили общемировое признание среди любителей, так что именно на них бегуны по всей планете проверяют свои силы и выносливость.
Можно подумать, что «пятёрка» и марафон – это короткая и длинная дистанции, однако нет: всё, что длиннее 3000 м, относится к стайерскому бегу.
Что такое стайерский бег, и в чём его особенности
Стайерский бег большинство людей знают под словосочетанием «бег на длинные дистанции». Марафон, «пятёрка», суточный бег и т.п. – всё это объединено под общим названием «стайерский бег».
В отличие от бега на средние дистанции и тем более спринтерского бега, в стайерском скорость выступает менее важным фактором, а вот темп и выносливость выходят на первое место. Чем длиннее дистанция, тем, разумеется, и меньше вероятность всплеска скорости, известного как «финишный рывок» в конце гонки.
Время тренировки и восстановления на длинных дистанциях намного больше, чем для средних и коротких пробегов. Так, если у спринтера или средневика вышла плохая гонка, то следующую можно повторить через неделю или меньше. С полумарафоном и тем более марафоном такого уже не получится.
Элитные марафонцы, к примеру, за год пробегают не более 1-2 целевых марафонов. Конечно, все системы организма восстанавливаются за 2-3 недели, но тренеры рекомендуют делать перерыв между целевыми марафонами на 5-6 месяцев. За этот срок атлет успевает восстановиться психологически и качественно подготовиться к следующей гонке.
Старт чемпионата России по полумарафонуКто такой стайер
Стайер – это бегун на соответствующие дистанции. Марафонец – это стайер, сверхмарафонец – тоже стайер, бегуны на 3 км – и они стайеры. Однако не всегда это слово подразумевает участие в забегах на длинные дистанции.
Термин «стайер» чаще всего означает генетическую предрасположенность человека к дистанциям длиннее 3000 метров. Бегуны на длинные дистанции достигают обычно 75–85% от максимального потребления кислорода, в то время как спринтеры доходят до 100%.
Тренировочные планы к марафону и полумарафону. Скачайте и начните подготовку сегодня.
Бегуны-дистанционщики могут отлично выступать как на длинных, так и на средних дистанциях. Например, Нильс Гундер Хэгг (Швеция) и Саид Ауита (Марокко) установили мировые рекорды как на 1500, так и на 5000 метров.
Например, Нильс Гундер Хэгг (Швеция) и Саид Ауита (Марокко) установили мировые рекорды как на 1500, так и на 5000 метров.
Дистанции в стайерском беге
Всё, что в беге составляет от 3000 метров и длиннее, – это стайерские, или длинные, дистанции. Всё, что короче 3000 метров, – средние дистанции. К слову, 3000 м относят и к тому, и к другому виду гонок.
Граница между двумя этими разделами бега – в нашем организме. На средних дистанциях гликоген только начинается расходоваться, а вот в марафонском беге происходит полное опустошение запасов гликогена, поэтому стайеры, особенно марафонцы, должны уделять особое внимание питанию.
Официальными дистанциями стайерского бега выступают:
- 3 км и 3000 м
- 4 км (кросс)
- 5 км и 5000 м
- 6 км (кросс)
- 8 км (кросс)
- 10 км и 10 000 м
- 12 км (кросс)
- 15 км
- 21,1 км
- 42,2 км
- 100 км
- Суточный бег
Все они включены в Единую всероссийскую спортивную классификацию. Нормативы можно посмотреть в таблице.
Нормативы можно посмотреть в таблице.
Кто-то спросит, почему мы разделили дистанции, к примеру, 5 км и 5000 м. Эти дистанции считаются разными дисциплинами лёгкой атлетики. 5 км – это бег по шоссе со своими нормативами и рекордами. 5000 м – дисциплина стадионная.
На Олимпийских играх награды разыгрываются на стадионных 5000 и 10 000 метрах. Из шоссейных дистанций в программу игр включён только марафон.
Техника стайерского бега
В отличие от спринтеров, стайеры бегут, двигаясь плавно и мягко. Наклон тела в таком беге почти отсутствует (наклон вперед примерно на 4-5°), движения рук менее энергичные, а угол сгибания локтевого сустава должен быть меньше, чем в других беговых дисциплинах, подъём колена маховой ноги не сильно выражен, очень важна экономичность движений и ритм дыхания, который рекомендуют согласовывать с частотой шагов.
К слову, брюшное дыхание, а не привычное грудное, для стайера подходит больше, поскольку при таком дыхании улучшается кровообращение.
В стайерском беге для уменьшения тормозящего действия предпочтительно ставить ногу с передней части стопы с перекатом на всю стопу. При отталкивании пятка должна быть поднятой несколько выше колена.
К концу дистанции некоторые спортсмены от усталости могут отклонять туловище назад, но знайте, что в таком положении сила отталкивания направляется больше вверх, что не способствует эффективности бега.
Разумеется, стайеры начинают бег с высокого старта. Стартовое ускорение после выстрела, конечно, делается, но его цель в том, чтобы занять выгодную позицию.
И хотя что 3-15 км, что марафон или суточный бег принадлежат к стану длинных дистанций, подготовка к ним будет кардинально отличаться. Даже 10 км пробегаются в менее интенсивном режиме, чем 5 км, которые преодолеваются практически на уровне МПК. В этом отношении дистанция 5 км или же 5000 м сложнее дистанций на 10 км и 10 000 м.
Читайте по теме: Техника бега на длинные дистанции: 5 основных правил
Особенности подготовки
Перечислим основные правила, работающие при подготовке для участия в забеге на длинную дистанцию.
Увеличивайте недельный тренировочный пробег не более чем на 10 % в неделю.
На тренировках иногда имитируйте целевой темп гонки. Допустим, вы хотите пробежать 10 км с темпом 4:30 мин/км. Для этого вам нужно бегать в таком темпе, однако нецелесообразно полностью имитировать гонку на тренировках, потому что это потребует длительного восстановления. Выход простой: бегите с целевым темпом дистанцию короче, делая интервалы с перерывом на отдых.
Начинайте каждую тренировку с 10 минут разминки: ходьбы или медленного бега. То же самое нужно сделать после окончания занятия.
Если во время бега у вас что-то болит два дня подряд, сделайте перерыв в своих пробежках, так как это может сигнализировать о начальном этапе травмы. Хорошая новость: даже пять дней полного отдыха от бега мало повлияют на ваш уровень физической подготовки.
Не ешьте и не пейте ничего ранее не испробованного до или во время гонки и тяжёлой тренировки.
Рельеф, встречный ветер могут замедлить ваш темп, но ключ в том, чтобы контролировать свои усилия, а не темп, поэтому не расстраивайтесь, если в ветреный день не можете достигнуть привычных значений.
Во время восстановительных пробежек вы должны сохранять способность говорить связными предложениями. Если вам тяжело, это сигнал снизить темп.
Сон – важная часть вашего прогресса, поэтому на каждую дополнительную милю (1609 м) спите одну дополнительную минуту. Если ваш недельный пробег составил 50 км, каждую ночь вы должны спать на полчаса дольше обычного. Среднестатистическому человеку требуется от 7,5 до 8 часов сна, но вы должны спать дольше, если тренируетесь много.
Не игнорируйте кросс-тренинг: велосипед, плавание, силовые тренировки. Это не только даст отдых основным мышцам, но и сделает вас более сильным и здоровым бегуном.
Лучший способ побороться за личный рекорд – это поддерживать равномерный темп от начала до конца. Большинство мировых рекордов на 10 000 метров и марафоне, установленных за последнее десятилетие, имеют равномерную раскладку по километрам.
Если бежать слишком быстро в начале гонки, почти всегда можно поплатиться за это после первой половины дистанции. Всё дело в накоплении лактата – он не успевал утилизироваться, когда в начале гонки вы бежали в темпе, который не можете поддерживать длительное время, то есть выше вашего лактатного порога.
Читайте подборку статей по теме:
Известные стайеры России и мира
В современной России фамилии Киселёва, Ядгарова, Ахмадеева, Никитина, Трофимовой, Седовой, Коробкиной известны всем увлечённым бегунам. Все они – элита нынешнего стайерского бега нашей страны.
фото: Беговое сообществоНа мировой арене шоссе и стадионом правят Кенениса Бекеле, Элиуд Кипчоге, Мо Фара, Пола Рэдклифф, Вивиан Черуйот, Тирунеш Дибаба. В ультра пальма первенства у Килиана Жорнета, Скотта Джурека, Камиллы Херрон.
У каждого из них не один мировой рекорд на той или иной дистанции, а темп их бега с трудом поддаётся пониманию для среднестатистического любителя бега.
В стайерском беге прослеживается общая тенденция, когда с возрастом многие спортсмены переходят с классических длинных дистанций 5000 и 10000 м на марафонские. Примеров тому много, но наиболее известные – Бекеле и Кипчоге, которые когда-то соревновались именно на дорожке стадиона.
Примеров тому много, но наиболее известные – Бекеле и Кипчоге, которые когда-то соревновались именно на дорожке стадиона.
В России из выступающих на сегодня бегунов пробуют себя на полумарафоне Владимир Никитин и Елена Коробкина – сильнейшие атлеты на дистанциях от 3000 м до 10 000 м.
Так, Владимир Никитин в 2020 году обновил рекорды страны на 3000 м и 5000 м в помещении, а в 2019 выиграл свой первый полумарафон «Северная столица». А Елена Коробкина в 2019 году на своём дебютном полумарафоне сразу же завоевала титул чемпионки страны.
2020 | Легкая атлетика. Маклафлин бьет рекорд на советской дистанции
На легкоатлетическом турнире Олимпийских игр в Токио в барьерном беге на круг творятся настоящие чудеса. Вслед за уникальным достижением Карстена Вархольма золото с феноменальным мировым рекордом (51,46) выиграла американка Сидни Маклафлин, сбросив с прежнего достижения почти полсекунды. Причем при этом она едва не уступила своей соотечественнице Далайле Мухаммад!
Вообще 400 м с барьерами всегда считались в каком смысле советской, а затем и российской дистанцией. Татьяна Сторожева, Татьяна Зеленцова, Анна Амбразене, Маргарита Пономарева, Мария Степанова и Юлия Печенкина – вот список тех бегуний из СССР и России, кто владел мировым рекордом. Причем достижение Печенкиной (52,34), установленное в 2003 году, продержалось целых 16 лет, пока его не побила Мухаммад, а затем и Маклафлин. Не стоит забывать и о золоте Олимпийских игр-2000 в Сиднее нынешней исполняющей обязанности президента Всероссийской федерации легкой атлетики Ирины Приваловой.
Татьяна Сторожева, Татьяна Зеленцова, Анна Амбразене, Маргарита Пономарева, Мария Степанова и Юлия Печенкина – вот список тех бегуний из СССР и России, кто владел мировым рекордом. Причем достижение Печенкиной (52,34), установленное в 2003 году, продержалось целых 16 лет, пока его не побила Мухаммад, а затем и Маклафлин. Не стоит забывать и о золоте Олимпийских игр-2000 в Сиднее нынешней исполняющей обязанности президента Всероссийской федерации легкой атлетики Ирины Приваловой.
К сожалению, сейчас в барьерном беге в стране наступил спад, поэтому команду ОКР в данной дисциплине в Токио никто не представлял. Но все равно 400 м с барьерами приковывали внимание, ведь уровень конкуренции был запредельным. Действующая рекордсменка планеты Маклафлин (51,90), Мухаммад и Фемке Бол из Нидерландов показывали по ходу сезона высочайший уровень результатов. А в Токио они превзошли все ожидания.
В финале на финишную прямую троица фаворитов выбежала почти вместе, чуть впереди была Мухаммад. Однако Маклафлин все же сумела ее догнать и благодаря ускорению после заключительного барьера перегнать. Мухаммад финишировала второй, также с фантастическим временем – 51,57, Бол показала 52,03, что стало рекордом Европы, еще две участницы финала побили личные достижения. Так что барьерный бег удался.
Главные героини олимпийского финала на 400 м с барьерами в Токио
Фото © Michael Steele
И, главное, Маклафлин вряд ли на это остановится. Ей всего 21 год, она потрясающе талантлива. Пять лет назад в Рио-де-Жанейро совсем юная Сидни выбыла в полуфинале, показав время почти на пять секунд, чем сейчас в Токио. Но уже к чемпионату мира-2018 в Дохе ворвалась в элиту, завоевав серебро в барьерном беге и золото в эстафете 4х400 м. «В 2016-м я сделала ошибку, позволив атмосфере Игр «проникнуть» в меня. Но на сей раз я сумела остаться в своем «пузыре».
По словам Маклафлин, на Играх-2020 она дистанцировалась от социальных сетей и постаралась как можно больше времени проводить в своей комнате, общаясь со своей семьей и друзьями. Что ж, такая тактика «пузыря» помогла – Сидней не расплескала энергию и выдала чудо-забег на Олимпийских играх. Не исключено, что именно она первой среди женщин сможет превзойти и отметку в 51 секунду. Хотя у 20-летней Бол наверняка свои виды на мировые рекорды, да 31-летнюю Мухаммад рано сбрасывать со счетов.
Что ж, такая тактика «пузыря» помогла – Сидней не расплескала энергию и выдала чудо-забег на Олимпийских играх. Не исключено, что именно она первой среди женщин сможет превзойти и отметку в 51 секунду. Хотя у 20-летней Бол наверняка свои виды на мировые рекорды, да 31-летнюю Мухаммад рано сбрасывать со счетов.
Все, что нужно знать об олимпийском турнире по легкой атлетике читайте здесь
Полное расписание смотрите здесь
2020 | Легкая атлетика: день рекордов на женской стометровке. Где смотреть и чего ждать от финала.
Самым важным событием для болельщиков команды ОКР в пятничной программе соревнований по легкой атлетике на Олимпийских играх в Токио стала не первая золотая медаль (ее выиграл на дистанции 10 000 метров у мужчин кениец Селемон Барега), а квалификация в прыжках в высоту. И серебряный призер последнего чемпионата мира Михаил Акименко, и обладатель бронзовой медали Дохи-2019 Илья Иванюк смогли отобраться в финал, который состоится в воскресенье, 1 августа.
В отборочном потоке B без ошибок обошлись только два спортсмена: чемпион мира из Катара, двукратный олимпийский призер Мутаз Баршим и канадец Джанго Ловетт. Лидирующий в мировом сезоне Иванюк (2,37 метра) обе заключительные высоты (2,25 и 2,28) смог преодолеть только со второй попытки. Ни затейпированное колено Ильи, ни сложности в секторе — не повод драматизировать ситуацию и исключать его из числа претендентов на медали. Привыкание к новому часовому поясу и стадиону прошло гладко далеко не только у высотника из команды ОКР: к примеру, не смог преодолеть квалификацию победитель последнего перед Олимпиадой этапа «Бриллиантовой лиги» Дональд Томас с Багамских островов.
Выступавший в группе A Михаил Акименко оказался единственным атлетом, не испытавшим проблем с преодолением планки ни на одной из четырех высот. Один из предстартовых фаворитов — белорус Максим Недосеков (также как Иванюк прыгал на 2,37 и побеждал на этапе «Бриллиантовой лиги») только с третьей попытки взял 2,25 и отобрался в финал с последнего зачетного тринадцатого места (организаторы приняли решение допустить туда всех спортсменов, преодолевших высоту 2,28).
Среди тех квалификационных соревнований, финалы в которых пройдут завтра (всего их будет три) самыми яркими получились забеги у женщин на дистанции 100 метров. Призерка чемпионата мира Мари-Жозе Та Лу из Кот-д’Ивуара показала лучший результат дня и установила рекорд Африки (10.78 секунды), быстрейшее время в истории швейцарского спринта в пятницу обновлялось дважды: сначала Муджинга Камбунджи (10.95), а затем чемпионка Европы на дистанции 60 метров Айла Дель Понте (10.91). Уверенно выступили также главные претендентки на завтрашнее олимпийское золото: 34-летняя олимпийская чемпионка Пекина-2008 Шелли-Энн Фрейзер-Прайс (10.84 — на 21 сотую медленнее ее же национального рекорда, установленного в этом году) и ее соотечественница с Ямайки — обладательница золотого спринтерского дубля Рио-2016 Элейн Томпсон (10.82).
Субботний финал у мужчин в метании диска пройдет без двукратного серебряного призера Игр Петра Малаховского.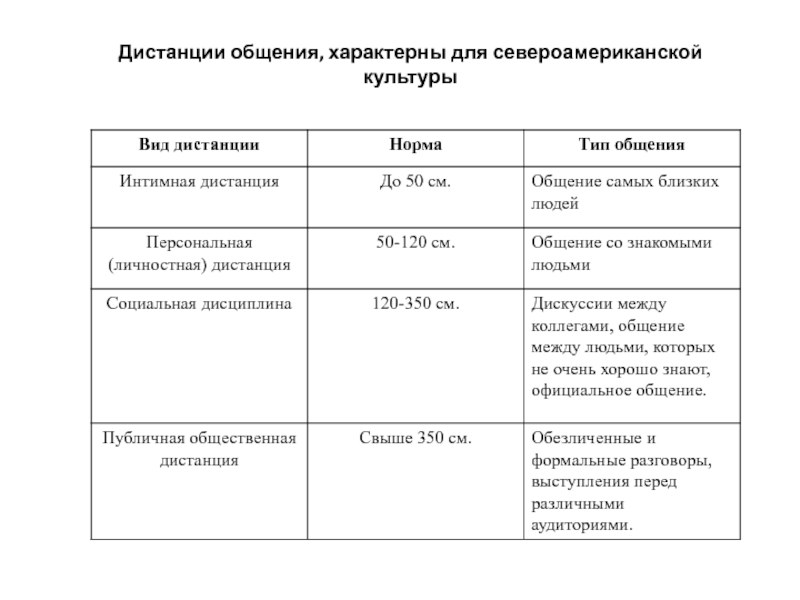 Польский гигант не смог преодолеть квалификацию. В его отсутствие на золото претендовать будут показавший лучший результат в квалификации (66.12 метра) чемпион мира из Швеции Даниэль Столь и чемпион Европы из Литвы Андрюс Гуджюс.
Польский гигант не смог преодолеть квалификацию. В его отсутствие на золото претендовать будут показавший лучший результат в квалификации (66.12 метра) чемпион мира из Швеции Даниэль Столь и чемпион Европы из Литвы Андрюс Гуджюс.
В финале дебютирующей в олимпийской программе смешанной эстафеты 4 по 400 метров в роли главных фаворитов выступит квартет из Польши, установивший сегодня рекорд Европы (3:10.44), теневые фавориты — Бельгия, использовавшая только одного джокера из семьи Борле (Жонатана).
Легкая атлетика на Олимпийских играх-2020 в Токио. Финалы. Расписание прямых трансляций
время начала — московское
31 июля, суббота
Мужчины. Метание диска. Начало в 14:15. («Россия-1», Первый)
Смешанная эстафета 4 по 400 метров. Начало в 15:35 («Россия-1»)
Женщины. 100 метров. Начало в 15:50 («Россия-1»)
Все, что нужно знать об олимпийском турнире по легкой атлетике читайте здесь
Полное расписание смотрите здесь
Шорт-трек
История шорт-трека в России началась с участия нашей страны во Всемирной универсиаде 1985 года в Беллуно (Италия). В 1982 году в Италии была закрыта Федерация конькобежного спорта. Итальянские спортсмены потеряли право представлять свою страну на соревнованиях в конькобежном спорте, поэтому было принято решение включить в программу Универсиады новый вид – дисциплину конькобежного спорта «шорт-трек». В СССР пришло приглашение собрать команду и принять участие в соревнованиях. Тогда в Советском Союзе никто не имел представления об этом виде спорта, поэтому спортсмены были отобраны из числа студентов-конькобежцев со спринтерским уклоном. Спортивный инвентарь закупили в Канаде.
В 1982 году в Италии была закрыта Федерация конькобежного спорта. Итальянские спортсмены потеряли право представлять свою страну на соревнованиях в конькобежном спорте, поэтому было принято решение включить в программу Универсиады новый вид – дисциплину конькобежного спорта «шорт-трек». В СССР пришло приглашение собрать команду и принять участие в соревнованиях. Тогда в Советском Союзе никто не имел представления об этом виде спорта, поэтому спортсмены были отобраны из числа студентов-конькобежцев со спринтерским уклоном. Спортивный инвентарь закупили в Канаде.
На Универсиаде 1985 наши спортсмены не показали медальных результатов. Однако уже в 1989 году на Универсиаде в Софии (Болгария) россиянка Марина Пылаева завоевала серебро на дистанции 1 500 м. В 1997 году на Универсиаде в Муджу (Южная Корея) россиянки выиграли две бронзовые медали – на дистанции 1 500 м усилиями Елены Тиханиной и в женской эстафете на 3 000 м. В 2009 году в Харбине (Китай) Руслан Захаров завоевал бронзу на 1 000 м. На зимней Универсиаде 2015 года, которая проходила в Словакии и Испании, сборная России по шорт-треку в составе Дмитрия Мясникова, Кирилла Шашина, Эдуарда Стрелкова и Тимура Захарова завоевала серебряную медаль в мужской эстафете на 5 000 метров.
В Алма-Ате (Казахстан) сборная России по шорт-треку в составе Артёма Денисова, Александра Коваля, Андрея Михасёва, Кирилла Шашина и Тимура Захарова завоевала серебро в эстафете на 5 000 м.
На зимних Универсиадах наши соотечественники выиграли три серебряные и три бронзовые награды.
Первый чемпионат СССР был проведен в 1988 году. Большинство членов первой сборной России по шорт-треку были воспитанниками Ленинградской школы шорт-трека. Первые медали России (СССР) в шорт-треке были получены на чемпионате мира 1991 года в Сиднее (Австралия), где советские спортсменки Наталья Исакова, Юлия Аллагулова, Юлия Власова и Марина Пылаева завоевали серебряные медали в эстафете на 3 000 м.
В России ежегодно проводятся два чемпионата по шорт-треку – по многоборью по программе чемпионатов мира и по отдельным дистанциям (олимпийским дисциплинам).
Следует отметить триумфальное выступление сборной России по шорт-треку на зимних Олимпийских играх в Сочи, когда команда в составе Виктора Ана, Семена Елистратова, Виктора Григорьева и Романа Захарова завоевали золото игр в эстафете на 5 000 м, Виктор Ан завоевал золото на дистанциях 1 000 м, 500 м и бронзу на дистанции 1 500 м, став самым титулованным спортсменом в шорт-треке. Виктор Григорьев завоевал серебро на дистанции 1 000 м. Российские спортсмены прочно удерживают ведущие позиции лидеров на европейских и мировых первенствах.
На последних зимних Олимпийских играх Семен Елистратов завоевал бронзовую награду на дистанции 1 500 м.
6. Дистанция. Основы делового общения
6. Дистанция
Касаясь вопросов соблюдения этикета во время делового общения, нельзя не упомянуть о дистанциях. Использование пространства человеком влияет на его способность соотносить себя с другими людьми, чувствовать их близкими себе или держать на расстоянии.
Выделяются четыре основные дистанции, которыми руководствуются большинство людей во время общения, это: интимная, личная, социальная и публичная.
Интимная дистанция может быть ближней, выражаясь прикосновением, и дальней – на расстоянии от 15 до 50 см. Ближняя интимная дистанция в деловой жизни предполагается во время рукопожатий, приветствий и прощаний. Во всех остальных случаях устанавливается дальняя дистанция – 50 см.
Личная дистанция – это деловое общение на расстоянии от 60 см до 1,2 м, к которому прибегают во время ведения бесед, переговоров, подписания контрактов. Такое расстояние ни к чему не обязывает и вместе с тем располагает к продолжению контракта.
Социальная дистанция – от 1,2 до 2,5 м – устанавливается в случаях, когда общение происходит с незнакомым человеком. На таком расстоянии директор принимает секретаря и других служащих, подчеркивая строго деловое общение. Подобная дистанция удобна, когда длительное общение нежелательно: можно отвести от собеседника взгляд, и на таком расстоянии это не будет означать прекращение разговора.
Публичная дистанция предполагает расстояние от 3,5 до 7,5 м. Она идеально подходит для выступлений на совещаниях, семинарах. Публичная дистанция – это расстояние от сцены до публики, характерное для театра; от трибуны до участников совещаний, собраний.
При общении с иностранными деловыми партнерами необходимо помнить, что представители разных национальных культур по-разному относятся к дистанции.
Англичане, американцы, скандинавы не терпят близких дистанций, рассматривая их как покушение на свое личное пространство. Японцы воспринимают прикосновение к себе как потерю самоконтроля со стороны собеседника или агрессивность, к ним не следует приближаться менее чем на 1 м. А французы легко переходят на близкую дистанцию, если вы их заинтересуете. Арабы, латиноамериканцы, греки, итальянцы, испанцы считают, что не прикасаться к собеседнику в разговоре – значит, холодно и недружелюбно вести себя по отношению к нему. Для них активная жестикуляция – норма.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес9 Измерения расстояния в науке о данных
Преимущества и недостатки обычных средств измерения расстояния
Измерения расстояния. Изображение автора.Многие алгоритмы, контролируемые или неконтролируемые, используют меры расстояния . Эти меры, такие как евклидово расстояние или косинусное сходство, часто можно найти в таких алгоритмах, как k-NN, UMAP, HDBSCAN и т. Д.
Понимание области измерения расстояния более важно, чем вы думаете. Возьмем, к примеру, k-NN — метод, часто используемый для обучения с учителем.По умолчанию часто используется евклидово расстояние. Само собой, мера расстояния большая.
Но что, если ваши данные очень многомерны? Будет ли тогда работать евклидово расстояние? Или что, если ваши данные состоят из геопространственной информации? Возможно, тогда лучшей альтернативой будет гаверсинусное расстояние!
Знание того, когда использовать какой измеритель расстояния, может помочь вам перейти от плохого классификатора к точной модели.
В этой статье мы рассмотрим многие меры расстояния и выясним, как и когда их лучше всего использовать.Самое главное, я буду говорить об их недостатках, чтобы вы могли понять, когда следует избегать определенных мер.
ПРИМЕЧАНИЕ : Для большинства дистанционных измерений можно было написать и были написаны длинные подробные статьи об их вариантах использования, преимуществах и недостатках. Я постараюсь охватить как можно больше, но могу потерпеть неудачу! Таким образом, рассматривайте эту статью как глобальный обзор этих мер.
Евклидово расстояние. Изображение автора.Мы начинаем с наиболее распространенной меры расстояния, а именно с евклидова расстояния.Это мера расстояния, которую лучше всего можно объяснить как длину отрезка, соединяющего две точки.
Формула довольно проста, поскольку расстояние вычисляется из декартовых координат точек с использованием теоремы Пифагора.
Евклидово расстояние НедостаткиНесмотря на то, что это обычная мера расстояния, евклидово расстояние не является инвариантным масштабом, что означает, что вычисленные расстояния могут быть искажены в зависимости от единиц измерения объектов.Как правило, перед использованием этой меры расстояния необходимо нормализовать данных.
Более того, по мере увеличения размерности ваших данных, евклидово расстояние становится менее полезным. Это связано с проклятием размерности, которое связано с представлением о том, что многомерное пространство не действует так, как мы интуитивно ожидаем от 2- или 3-мерного пространства. Чтобы получить хорошее резюме, см. Этот пост.
Варианты использования
Евклидово расстояние отлично работает, когда у вас есть данные малой размерности и важно измерить величину векторов.Такие методы, как kNN и HDBSCAN, сразу показывают отличные результаты, если евклидово расстояние используется для низкоразмерных данных.
Хотя многие другие меры были разработаны для учета недостатков евклидова расстояния, оно по-прежнему остается одной из наиболее часто используемых мер расстояния по уважительным причинам. Он невероятно интуитивно понятен в использовании, прост в реализации и показывает отличные результаты во многих случаях использования.
Косинусное расстояние. Изображение автора.Косинусное подобие часто использовалось как способ противодействовать проблеме евклидова расстояния с высокой размерностью.Косинусное подобие — это просто косинус угла между двумя векторами. Он также имеет тот же внутренний продукт векторов, если они были нормализованы так, чтобы оба имели длину один.
Два вектора с абсолютно одинаковой ориентацией имеют косинусное сходство, равное 1, тогда как два вектора, диаметрально противоположных друг другу, имеют сходство, равное -1. Обратите внимание, что их величина не имеет значения, поскольку это мера ориентации.
Косинусное подобиеНедостатки
Одним из основных недостатков косинусного подобия является то, что не учитывается величина векторов, а учитывается только их направление.На практике это означает, что различия в ценностях не учитываются полностью. Если взять, например, рекомендательную систему, то косинусное сходство не учитывает разницу в шкале оценок между разными пользователями.
Примеры использования
Мы часто используем косинусное сходство, когда у нас есть многомерные данные и когда величина векторов не имеет значения. Для анализа текста этот показатель довольно часто используется, когда данные представлены количеством слов.Например, когда слово чаще встречается в одном документе, чем в другом, это не обязательно означает, что один документ более связан с этим словом. Может случиться так, что документы имеют разную длину, и величина подсчета менее важна. Тогда лучше всего использовать косинусное подобие, которое не учитывает величину.
Расстояние Хэмминга. Изображение автора.Расстояние Хэмминга — это количество значений, которые различаются между двумя векторами. Обычно он используется для сравнения двух двоичных строк одинаковой длины.Его также можно использовать для строк, чтобы сравнить, насколько они похожи друг на друга, путем вычисления количества символов, которые отличаются друг от друга.
Недостатки
Как и следовало ожидать, расстояние Хэмминга трудно использовать, когда два вектора не равной длины. Вы можете сравнить векторы одинаковой длины друг с другом, чтобы понять, какие позиции не совпадают.
Более того, он не принимает во внимание фактическую стоимость, если они разные или равные.Поэтому не рекомендуется использовать эту меру расстояния, когда величина является важной мерой.
Варианты использования
Типичные варианты использования включают исправление / обнаружение ошибок при передаче данных по компьютерным сетям. Его можно использовать для определения количества искаженных битов в двоичном слове как способа оценки ошибки.
Кроме того, вы также можете использовать расстояние Хэмминга для измерения расстояния между категориальными переменными.
Манхэттенская дистанция. Изображение автора.Манхэттенское расстояние, часто называемое расстоянием такси или расстоянием городского квартала, вычисляет расстояние между векторами с действительными значениями. Представьте себе векторы, описывающие объекты на однородной сетке, например, на шахматной доске. Тогда манхэттенское расстояние относится к расстоянию между двумя векторами, если они могут двигаться только под прямым углом. При расчете расстояния не используется диагональное движение.
Манхэттенское расстояниеНедостатки
Хотя манхэттенское расстояние кажется приемлемым для многомерных данных, это мера, которая несколько менее интуитивно понятна, чем евклидово расстояние, особенно при использовании в многомерных данных.
Более того, оно с большей вероятностью даст более высокое значение расстояния, чем евклидово расстояние, поскольку оно не является кратчайшим из возможных. Это не обязательно вызывает проблемы, но вы должны это учитывать.
Варианты использования
Когда ваш набор данных имеет дискретные и / или двоичные атрибуты, Manhattan, кажется, работает достаточно хорошо, поскольку он учитывает пути, которые реально можно было бы выбрать в пределах значений этих атрибутов. Возьмем, к примеру, евклидово расстояние, которое создаст прямую линию между двумя векторами, хотя на самом деле это может быть невозможно.
Чебышевская дистанция. Изображение автора.Расстояние Чебышева определяется как наибольшая разница между двумя векторами по любому координатному измерению. Другими словами, это просто максимальное расстояние по одной оси. Из-за своей природы его часто называют расстоянием до шахматной доски, поскольку минимальное количество ходов, необходимых королю для перехода с одного поля на другое, равно расстоянию Чебышева.
Расстояние ЧебышеваНедостатки
Чебышев обычно используется в очень специфических случаях использования, что затрудняет его использование в качестве универсальной метрики расстояния, такой как евклидово расстояние или косинусное подобие.По этой причине рекомендуется использовать его только тогда, когда вы абсолютно уверены, что он подходит для вашего варианта использования.
Варианты использования
Как упоминалось ранее, расстояние Чебышева можно использовать для извлечения минимального количества ходов, необходимых для перехода от одного квадрата к другому. Более того, это может быть полезной мерой в играх, допускающих неограниченное 8-стороннее движение.
На практике расстояние Чебышева часто используется в складской логистике, поскольку оно очень похоже на время, необходимое мостовому крану для перемещения объекта.
Расстояние Минковского. Изображение автора.Расстояние Минковского — более сложная мера, чем большинство других. Это метрика, используемая в нормированном векторном пространстве (n-мерное реальное пространство), что означает, что ее можно использовать в пространстве, где расстояния могут быть представлены как вектор, имеющий длину.
Эта мера имеет три требования:
- Нулевой вектор — нулевой вектор имеет нулевую длину, тогда как любой другой вектор имеет положительную длину. Например, если мы путешествуем из одного места в другое, то это расстояние всегда положительно.Однако, если мы путешествуем из одного места в себя, то это расстояние равно нулю.
- Скалярный коэффициент — Когда вы умножаете вектор на положительное число, его длина изменяется, при этом направление сохраняется. Например, если мы пройдем определенное расстояние в одном направлении и добавим такое же расстояние, направление не изменится.
- Неравенство треугольника — Кратчайшее расстояние между двумя точками — прямая линия.
Формула для расстояния Минковского показана ниже:
Расстояние Минковского Самым интересным в этой мере расстояния является использование параметра p .Мы можем использовать этот параметр, чтобы управлять показателями расстояния, чтобы они были похожи на другие.
Общие значения p :
- p = 1 — Манхэттенское расстояние
- p = 2 — Евклидово расстояние
- p = ∞ — Расстояние Чебышева
Недостатки
Минковский имеет те же недостатки, что и Они представляют собой меры расстояния, поэтому очень важно хорошее понимание таких метрик, как манхэттенское, евклидово и расстояние Чебышева.
Более того, с параметром p на самом деле может быть проблематично работать, поскольку поиск правильного значения может быть довольно неэффективным с вычислительной точки зрения в зависимости от вашего варианта использования.
Варианты использования
Положительным моментом p является возможность перебрать его и найти меру расстояния, которая лучше всего подходит для вашего варианта использования. Это дает вам огромную гибкость в отношении метрики расстояния, что может быть огромным преимуществом, если вы хорошо знакомы с p и многими мерами расстояния.
Индекс Жаккара (или пересечение по объединению) — это показатель, используемый для вычисления сходства и разнообразия наборов выборок. Это размер пересечения, деленный на размер объединения наборов выборок.
На практике это общее количество похожих объектов между наборами, деленное на общее количество объектов. Например, если у двух наборов есть 1 общая сущность и всего 5 разных сущностей, то индекс Жаккара будет 1/5 = 0.2.
Для вычисления расстояния Жаккара мы просто вычитаем индекс Жаккара из 1:
Расстояние ЖаккарНедостатки
Основным недостатком индекса Жаккара является то, что на него сильно влияет размер данных. Большие наборы данных могут иметь большое влияние на индекс, поскольку они могут значительно увеличить объединение, сохраняя при этом пересечение схожим.
Примеры использования
Индекс Жаккара часто используется в приложениях, где используются двоичные или двоичные данные.Если у вас есть модель глубокого обучения, прогнозирующая сегменты изображения, например автомобиля, индекс Жаккара можно затем использовать для расчета, насколько точно этот прогнозируемый сегмент соответствует истинным меткам.
Точно так же его можно использовать в анализе схожести текста, чтобы измерить, насколько часто выбираются слова между документами. Таким образом, его можно использовать для сравнения наборов шаблонов.
Хаверсинское расстояние. Изображение автора.Хаверсинус — это расстояние между двумя точками на сфере с учетом их долготы и широты.Это очень похоже на евклидово расстояние в том, что вычисляет самую короткую линию между двумя точками. Основное отличие состоит в том, что прямая линия невозможна, поскольку здесь предполагается, что две точки находятся на сфере.
Расстояние Гаверсинуса между двумя точкамиНедостатки
Одним из недостатков этой меры расстояния является то, что предполагается, что точки лежат на сфере . На практике это бывает редко, поскольку, например, земля не идеально круглая, что в некоторых случаях может затруднить расчет.Вместо этого было бы интересно взглянуть на расстояние Винсенти , которое вместо этого предполагает эллипсоид.
Примеры использования
Как и следовало ожидать, расстояние Гаверсина часто используется в навигации. Например, вы можете использовать его для расчета расстояния между двумя странами при перелете между ними. Обратите внимание, что это гораздо менее подходит, если расстояния сами по себе уже не так велики. Кривизна не будет иметь такого большого воздействия.
Коэффициент Соренсена – Дайса.Изображение автора.Индекс Соренсена-Дайса очень похож на индекс Жаккара в том, что он измеряет сходство и разнообразие наборов выборок. Хотя они рассчитываются аналогично, индекс Соренсена-Дайса немного более интуитивно понятен, потому что его можно увидеть как процент перекрытия между двумя наборами, который представляет собой значение от 0 до 1:
Коэффициент Соренсена-ДайсаНедостатки
Как и у Жаккарда index, они оба преувеличивают важность наборов, в которых практически нет основополагающих истинно-положительных наборов.В результате он может доминировать над средней оценкой, полученной по нескольким сетам. Он взвешивает каждый элемент обратно пропорционально размеру соответствующего набора, а не обрабатывает их одинаково.
Сценарии использования
Сценарии использования аналогичны, если не совпадают, с индексом Жаккарда. Вы обнаружите, что он обычно используется либо в задачах сегментации изображений, либо в анализе сходства текста.
ПРИМЕЧАНИЕ: Существует гораздо больше мер расстояния, чем 9, упомянутых здесь. Если вы ищете более интересные показатели, я бы посоветовал вам изучить один из следующих: Махаланобис, Канберра, Брайкуртис и KL-дивергенция.
Если вы, как и я, увлечены искусственным интеллектом, наукой о данных или психологией, не стесняйтесь добавлять меня в LinkedIn или подписываться на меня в Twitter.
Типы дистанций в машинном обучении | пользователя Ujjainee De | Аналитика Vidhya
Вы когда-нибудь задумывались, как алгоритмы машинного обучения вычисляют расстояние? Или на этот раз вам пришло в голову, что существует более одного способа рассчитать расстояние?
Когда вы читаете слово «Расстояние», вы вспоминаете основное определение этого слова, которое гласит, что это числовое измерение того, насколько далеко друг от друга находятся объекты или точки.Но когда вы слышите это слово вместе с машинным обучением, вы можете подумать, что это другое, и угадайте, что? Это!
Когда мы говорим о расстоянии, мы имеем в виду метрику расстояния. А базовое математическое определение, метрика расстояния, использует функцию расстояния, которая обеспечивает метрику отношения между каждым элементом в наборе данных .
Несколько алгоритмов машинного обучения — контролируемые или неконтролируемые, используют метрики расстояния, чтобы узнать шаблон входных данных для принятия любого решения на основе данных.Хорошая метрика расстояния помогает значительно повысить производительность процессов классификации, кластеризации и поиска информации.
Существует множество показателей расстояния, но в этой статье мы обсудим только несколько широко используемых показателей расстояния. Сначала мы попытаемся понять математику, лежащую в основе этих показателей, а затем определим алгоритмы машинного обучения, в которых мы используем эти показатели расстояния.
Ниже приведены наиболее часто используемые метрики расстояния —
Когда мы думаем о расстоянии, мы обычно представляем расстояния между городами.Это наиболее интуитивное понимание концепции расстояния. К счастью, этот пример идеально подходит для объяснения ограничений расстояний Минковского. Мы можем вычислить расстояние Минковского только в нормированном векторном пространстве, что является причудливым способом сказать: «в пространстве, где расстояния могут быть представлены как вектор, имеющий длину».
Начнем с доказательства того, что карта является векторным пространством. Если мы возьмем карту, мы увидим, что расстояния между городами — это нормированное векторное пространство, потому что мы можем нарисовать вектор, который соединяет два города на карте.Мы можем объединить несколько векторов, чтобы создать маршрут, который соединяет более двух городов. Теперь прилагательное «нормированный». Это означает, что вектор имеет свою длину и ни один вектор не имеет отрицательной длины. Это ограничение также соблюдается, потому что, если мы проведем линию между городами на карте, мы сможем измерить ее длину.
Опять же, нормированное векторное пространство — это векторное пространство, в котором определена норма. Предположим, что X — векторное пространство, тогда норма на X — вещественная функция || x ||, что удовлетворяет следующим условиям —
- Нулевой вектор — Нулевой вектор будет иметь нулевую длину. Сказать: если мы посмотрим на карту, это очевидно. Расстояние от города до того же города равно нулю, потому что нам совсем не нужно путешествовать. Расстояние от города до любого другого города положительно, потому что мы не можем проехать -20 км.
- Скалярный коэффициент — Направление вектора не меняется, когда вы умножаете его на положительное число, хотя его длина будет изменена. Пример: мы проехали 50 км на север. Если мы проедем еще 50 км в том же направлении, мы окажемся на 100 км севернее.Направление не меняется.
- Неравенство треугольника — Если расстояние является нормой, то вычисленное расстояние между двумя точками всегда будет прямой линией.
Вам может быть интересно, зачем нам нормированный вектор, не можем ли мы просто не использовать простые метрики? Нормированный вектор обладает указанными выше свойствами, которые помогают поддерживать однородность метрики, индуцированную нормой, и инвариантность трансляции.
Расстояние можно рассчитать по следующей формуле —
Расстояние Минковского — это обобщенная метрика расстояния.Здесь обобщенное означает, что мы можем манипулировать приведенной выше формулой для вычисления расстояния между двумя точками данных по-разному.
Как упоминалось выше, мы можем манипулировать значением p и вычислять расстояние тремя разными способами:
p = 1, Манхэттенское расстояние
p = 2, Евклидово расстояние
p = ∞ , Расстояние Чебычева (не будет обсуждаться в этой статье)
Мы используем Манхэттенское расстояние, если нам нужно рассчитать расстояние между двумя точками данных в сетке.Как упоминалось выше, мы используем формулу расстояния Минковского , чтобы найти расстояние Манхэттена, задав значение p’s как 1 .
Допустим, мы хотим вычислить расстояние, d , между двумя точками данных — x и y .
Расстояние d будет рассчитано с использованием абсолютной суммы разницы между его декартовыми координатами, как показано ниже:
где, n- количество переменных, xi и yi — переменные векторов x и y соответственно в двумерном векторном пространстве.т.е. x = (x1, x2, x3,…) и y = (y1, y2, y3,…) .
Теперь расстояние d будет рассчитано как-
(x1 — y1) + (x2 — y2) + (x3 — y3) +… + (xn — yn) .
Если вы попытаетесь визуализировать расчет расстояния, он будет выглядеть примерно так:
Манхэттенское расстояние также известно как геометрия такси, расстояние между кварталом и т. Д.
Когда мы можем использовать карту города, мы можем указывать направление, говоря людям, что они должны пройти два городских квартала на север, затем повернуть налево и проехать еще три городских квартала. В общей сложности они проедут пять городских кварталов, что составляет манхэттенское расстояние между отправной точкой и пунктом назначения.
Также известна как «Манхэттенское расстояние» или «Норма такси». Норма L1 — это сумма модулей векторов в пространстве. Это наиболее естественный способ измерения расстояния между векторами, то есть суммы абсолютных разностей компонентов векторов.В этой норме все компоненты вектора имеют одинаковый вес.
Имея, например, вектор X = [3,4]:
Норма L1 вычисляется по
Как вы можете видеть на графике, норма L1 — это расстояние, которое вам нужно пройти между исходной точкой (0 , 0) в пункт назначения (3,4) таким образом, как такси проезжает между кварталами города, чтобы прибыть в пункт назначения.
Евклидово расстояние — одна из наиболее часто используемых метрик расстояния. Он рассчитывается по формуле Расстояние Минковского путем установки значения p’s на 2 .Это обновит формулу расстояния d ’ , как показано ниже.
Формула евклидова расстоянияможет использоваться для вычисления расстояния между двумя точками данных на плоскости.
Если мы снова посмотрим на пример городского квартала, использованный для объяснения расстояния до Манхэттена, мы увидим, что пройденный путь состоит из двух прямых линий. Когда мы проводим еще одну прямую линию, соединяющую начальную и конечную точки, мы получаем треугольник. В этом случае расстояние между точками можно рассчитать с помощью теоремы Пифагора.
Это самая популярная норма, также известная как евклидова норма. Это кратчайшее расстояние от одной точки до другой.
Используя тот же пример, норма L2 рассчитывается по
Как вы можете видеть на графике, норма L2 является наиболее прямым маршрутом.
Есть одно соображение, которое следует принять в отношении нормы L2, и это то, что каждый компонент вектора возведен в квадрат, а это означает, что выбросы имеют больший вес, поэтому они могут исказить результаты.
Расстояние Хэмминга в информационных технологиях представляет собой количество точек, в которых два соответствующих фрагмента данных могут отличаться.Он часто используется для различных видов исправления ошибок или оценки контрастирующих строк или фрагментов данных.
Хотя на первый взгляд это может показаться сложным и неясным, расстояние Хэмминга — очень практичный показатель для измерения строк данных. Расстояние Хэмминга включает в себя подсчет того, какие наборы соответствующих цифр или мест различны, а какие совпадают. Например, возьмите текстовую строку «hello world» и сравните ее с другой текстовой строкой «herra poald». Вдоль соответствующих строк есть пять мест, где буквы разные.
Почему это важно? Одно из фундаментальных применений расстояния Хэмминга — корректировка двоичного кода в сторону того или иного результата. Профессионалы говорят об однобитовых или двухбитовых ошибках, идее о том, что поврежденные данные могут быть преобразованы в правильный исходный результат. Проблема в том, что если есть две строки и один поврежденный фрагмент данных, необходимо выяснить, к какому окончательному результату ближе всего поврежденный или третий набор данных. Вот здесь-то и пригодится расстояние Хэмминга — например, если расстояние Хэмминга равно четырем и есть однобитовая ошибка в отношении одного результата, наиболее вероятно, что это правильный результат.Это лишь одно из приложений, которое может иметь расстояние Хэмминга для оценки кода и строки данных.
Предположим, что есть две строки 1101 1001 и 1001 1101.
11011001 ⊕ 10011101 = 01000100. Поскольку это содержит две единицы, расстояние Хэмминга, d (11011001, 10011101) = 2.
В наборе Для строк равной длины минимальное расстояние Хэмминга — это наименьшее расстояние Хэмминга между всеми возможными парами строк в этом наборе.
Есть два термина: сходство и расстояние.Они обратно пропорциональны друг другу, т. Е. Если одно увеличивается, другое уменьшается, и наоборот. формула для которого:
1-cos_sin = cos_distance
Формула подобия косинуса может быть получена из уравнения скалярных произведений: —
Теперь вы должны думать, какое значение угла косинуса поможет обнаружить сходство .
Теперь, когда у нас есть значения, которые будут рассматриваться для измерения сходства, нам нужно знать, что означают 1, 0 и -1.
Здесь значение косинуса 1 соответствует векторам, указывающим в одном направлении, т.е. между документами / точками данных есть сходство. На нуле для ортогональных векторов, т. Е. Несвязанных (обнаружено некоторое сходство). Значение -1 для векторов, указывающих в противоположных направлениях (Нет сходства).
Чтобы найти косинусное расстояние, нам просто нужно ввести значения в формулу и вычислить.
Этот раздел призван помочь понять использование показателей расстояния в моделировании машинного обучения на примерах.
K-Nearest Neighbours (KNN) —
KNN — это не вероятностный алгоритм обучения с учителем, т.е. он не дает вероятности принадлежности к какой-либо точке данных, а KNN классифицирует данные по жесткому назначению, например, точка данных будет либо принадлежать 0, либо 1. KNN использует метрики расстояния для поиска сходств или различий.
На примере набора данных радужной оболочки глаза, который имеет три класса, мы увидим, как KNN будет идентифицировать классы для тестовых данных.
На изображении №2 над черным квадратом показана точка тестовых данных.Теперь нам нужно определить, к какому классу принадлежит эта точка тестовых данных, с помощью алгоритма KNN.
Чтобы найти ближайших соседей, мы используем метрики расстояния. Сначала мы вычисляем расстояние между каждым поездом и точкой тестовых данных, а затем выбираем верхнюю ближайшую в соответствии со значением k ( K — количество ближайших соседей точки тестовых данных. Эти K точек данных затем будут использоваться для определить класс для точки тестовых данных.)
Учитывая этот код,
# Создать модельKNN_Classifier = KNeighborsClassifier (n_neighbors = 6, p = 2, metric = 'minkowski')
Мы используем метрику расстояния Минковского с значение p как 2 i.е. Классификатор KNN будет использовать формулу метрики евклидова расстояния .
По мере продвижения в моделировании машинного обучения теперь мы можем обучить нашу модель и начать прогнозирование класса для тестовых данных.
# Тренируйте модель
KNN_Classifier.fit (x_train, y_train) # Давайте спрогнозируем классы для тестовых данных
pred_test = KNN_Classifier.predict (x_test)
После того, как выбраны самые ближайшие соседи, мы проверяем наиболее проголосовавший класс в соседях —
На изображении выше, это класс 1, так как он получил наибольшее количество голосов.
На этом небольшом примере мы увидели, насколько важна метрика расстояния для классификатора KNN. Это помогло нам получить ближайшие точки данных поезда, для которых были известны классы.
K-means:
В алгоритмах классификации, вероятностных или не вероятностных, нам будут предоставлены помеченные данные, чтобы было легче предсказать классы. Хотя в алгоритме кластеризации у нас нет информации о том, какая точка данных принадлежит какому классу. Метрики расстояния — важная часть такого алгоритма.
В K-средних мы выбираем несколько центроидов, которые определяют количество кластеров. Затем каждой точке данных будет присвоен ближайший к ней центроид с использованием метрики расстояния (евклидова) . Мы будем использовать данные радужной оболочки глаза, чтобы понять основной процесс K-средних.
На изображении №1 выше, как вы можете видеть, мы случайным образом разместили центроиды, а на изображении №2, используя метрику расстояния, мы попытались найти их ближайший класс кластера.
Как мы видели в приведенном выше примере, не имея каких-либо знаний о метках с помощью метрики расстояния в K-средних, мы сгруппировали данные в 3 класса, просто используя алгоритмы.Таким образом, снова важны показатели расстояния.
Поиск информации
При поиске информации мы работаем с неструктурированными данными. С помощью методов, используемых в НЛП, мы можем создавать векторные данные таким образом, чтобы их можно было использовать для получения информации при запросе. После преобразования неструктурированных данных в векторную форму мы можем использовать показатель сходства , косинус , чтобы отфильтровать нерелевантные документы из корпуса.
Как только человек углубится в машинное обучение или анализ данных или в любую область науки о данных, ему / ей потребуются глубокие знания расстояний, доступных в курсе, чтобы использовать правильные метрики расстояния в нужном месте. для достижения наилучшего результата.Следовательно, эта статья направлена на то, чтобы предоставить людям знания о некоторых популярных показателях расстояния / сходства и о том, как и где их можно использовать для решения сложных задач машинного обучения.
«Различные типы дистанций, используемые в машинном обучении» | Автор: Чандрима Саркар
Термин «показатели расстояния» получил множество определений среди специалистов по математике, статистике и машинному обучению. В результате эти термины, концепции и их использование вышли далеко за рамки.Метрики расстояния очень важны в машинном обучении для принятия правильного решения на основе данных. Выбор хорошей метрики расстояния важен для распознавания сходства между содержимым. В этом моем блоге рассматриваются различные типы расстояний и их использование в машинном обучении.
Чтобы определить расстояние Минковского, нам нужно выучить некоторые математические термины. Они включают следующие:
- Векторное пространство: Это представляет собой набор объектов, называемых векторами, которые можно складывать вместе и умножать на числа ( также называется скалярами ).
- Норма: Норма — это функция, которая назначает строго положительную длину каждому вектору в векторном пространстве (единственное исключение — нулевой вектор, длина которого равна нулю). Обычно обозначается как ∥x∥.
- Нормированное векторное пространство: Это — векторное пространство над действительными или комплексными числами, на котором определена норма.
Расстояние Минковского определяется как метрика подобия между двумя точками в нормированном векторном пространстве.Он представлен формулой
Он также представляет собой обобщенную метрику, которая включает евклидово и манхэттенское расстояние. Мы можем управлять значением p и вычислять расстояние тремя различными способами, также известными как форма Lp.
- p = 1, Манхэттенское расстояние
- p = 2, Евклидово расстояние
- p = ∞, Чебычевское расстояние
Где это используется?
Расстояние Минковского часто используется, когда интересующие переменные измеряются на шкалах отношений с абсолютным нулевым значением.
Когда мы говорим о расстояниях, мы в основном думаем о них как о более или менее прямой линии. Если мы думаем о перелете из одного города в другой, мы думаем о том, сколько километров нам нужно преодолеть самолетом. Эти примеры расстояний которые мы можем придумать, являются примерами евклидова расстояния . По сути, он измеряет длину сегмента, соединяющего две точки.
Евклидово расстояниеПомните теорему Пифагора из уроков математики?
Теорема ПифагораТеорема Пифагора дает это расстояние между двумя точками.Мы можем получить уравнение для евклидова расстояния, подставив p = 2 в формулу расстояния Минковского. Его также называют нормой L2.
Бывают ситуации, когда евклидово расстояние не дает нам правильной метрики. В этих случаях нам необходимо использовать функции расстояния, упомянутые ниже.
Допустим, мы хотим вычислить расстояние между двумя кварталами в городе. На этот раз мы рассчитаем расстояние в виде сетки, которая представляет различные кварталы в городе.
Манхэттен РасстояниеПредположим, мы хотим проехать от блока A до блока B в городе. Расстояние, пройденное от блока A до блока B, называется манхэттенским расстоянием.
Мы можем получить уравнение для манхэттенского расстояния, если подставим p = 1 в формулу расстояния Минковского. Он также назывался L1 norm .
Манхэттенское расстояние также известно как геометрия такси, расстояние до городских кварталов и т. Д.
Где используется евклидово и манхэттенское расстояние?
Манхэттенское и Евклидово расстояния используются в задачах регрессии и классификации.Но евклидово расстояние не подходит для данных большой размерности. Это происходит из-за того, что известно как «проклятие размерности». Проклятие размерности относится к различным явлениям, которые возникают при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), которые не происходят в низкоразмерных средах, таких как трехмерное физическое пространство повседневного опыта. В данных большого размера предпочтительнее расстояние Манхэттена. Кроме того, если вы вычисляете ошибки, Манхэттенское расстояние полезно, когда вы хотите выделить выбросы из-за его линейного характера.
Расстояние Хэмминга — это метрика для сравнения двух строк двоичных данных. При сравнении двух двоичных строк одинаковой длины расстояние Хэмминга — это количество битовых позиций, в которых эти два бита различаются. Расстояние Хэмминга между двумя строками, a и b, обозначается как d (a, b).
Расчет расстояния Хэмминга:
Чтобы вычислить расстояние Хэмминга между двумя строками, мы выполняем их операцию XOR (a⊕ b), а затем подсчитываем общее количество единиц в результирующей строке.
Предположим, что есть две строки 1101 1001 и 1001 1101.
11011001 ⊕ 10011101 = 01000100. Поскольку это содержит две единицы, расстояние Хэмминга, d (11011001, 10011101) = 2.
Другой пример расстояния ХэммингаИспользование расстояния Хэмминга:
Расстояние Хэмминга используется для исправления ошибок ближайших соседей. Исправление ошибок ближайшего соседа включает в себя сначала определение кодовых слов, обычно обозначаемых как C, которые известны как источнику, так и приемнику.После идентификации неправильного кодового слова ближайший сосед вычисляет расстояние Хэмминга между ним и каждым кодовым словом, содержащимся в C. Кодовое слово с наименьшим расстоянием Хэмминга имеет наибольшую вероятность быть правильным.
Чтобы определить, насколько похожи два документа или любой тип объекта, мы используем косинус сходства . Для его вычисления нам нужно измерить косинус угла между двумя векторами. Косинусное расстояние и Косинусное сходство обратно пропорциональны друг другу.Если косинусное расстояние увеличивается, косинусное сходство уменьшается, и наоборот. Следовательно, две точки, расположенные близко друг к другу, обладают схожими свойствами, чем точки, находящиеся далеко друг от друга.
Косинусное подобие = cosθ
Косинусное расстояние = 1-cosθ.
На приведенном выше рисунке угол, образованный двумя линиями A и B, составляет 45 °. Следовательно, косинусное сходство равно cos 45 °, что приблизительно равно 0,53, что означает, что точки схожи на 53%.Косинусное расстояние будет (1–0,53), что равно 0,47. Значение подобия косинуса должно находиться в диапазоне от -1 до +1.
Где используются косинусное расстояние и косинусное подобие?
Косинусное расстояние и косинусное подобие используются в рекомендательных системах.
Давайте рассмотрим систему рекомендаций по фильмам. Взяв жанр «боевик» по оси X и жанр «комедия» по оси Y, возьмем два фильма, такие как «Мстители», которые относятся к жанру «боевик», и другой. , скажите «Гадкий я», который относится к жанру «комедия».«Таким образом, мы можем нанести точки, учитывая названия фильмов, как (0,1) и (1,0) соответственно. Точка (0,1) означает, что фильм не столько боевик, сколько комедия. Таким образом, две точки имеют нулевое сходство, что означает cos 90 °. Поэтому система рекомендаций по фильмам не порекомендует тех, кто любит фильмы жанра «комедия» с фильмами жанра «боевик».
Точно так же, если мы возьмем такие фильмы, как «Гадкий я» и «История игрушек» на оси Y с координатами (0,0.9) и (0,1), угол между ними равен 0 °, что означает косинусное сходство 1 (cos 0 °).Поэтому система рекомендует пользователю посмотреть «Гадкий я», если он уже смотрел «Историю игрушек».
В конце этого блога мы узнали о различных показателях расстояния и их использовании в машинном обучении. Надеюсь, это будет полезно для людей, которые занимаются машинным обучением / наукой о данных.
Краткий обзор формулСпасибо за внимание 🙂
.
Различные типы измерения расстояния в машинном обучении
В этом посте вы узнаете о различных типах мер расстояния , используемых в различных алгоритмах машинного обучения , таких как K-ближайших соседей, K-средних и т. Д.
Меры расстояния используются для измерения сходства между двумя или более векторами в многомерном пространстве. Ниже представлены различные формы метрик / мер расстояния:
- Геометрические расстояния
- Вычислительные расстояния
- Статистические расстояния
Геометрические измерения расстояний
Геометрические метрики расстояния, в первую очередь, имеют тенденцию измерять сходство между двумя или более векторами исключительно на основе расстояния между двумя точками в многомерном пространстве.Примерами таких геометрических мер расстояния являются расстояние Минковского, Евклидово расстояние и Манхэттенское расстояние. Еще одна другая форма геометрического расстояния — это косинусное подобие, о котором мы поговорим в этом разделе.
Расстояние Минковского — это общая форма расстояния Евклида и Манхэттена. Математически это можно представить следующим образом:
Рис. 1. Формула расстояния МинковскогоКогда значение P становится равным 1, это называется манхэттенским расстоянием.Когда P принимает значение 2, оно становится евклидовым расстоянием. Давайте разберемся с этими мерами расстояния с наглядными диаграммами.
Евклидово расстояние
Формула евклидова расстояния выглядит следующим образом. Он формируется путем присвоения значения P равного 2 в формуле расстояния Минковского.
Рис. 2. Формула евклидова расстоянияДавайте посмотрим на другой иллюстративный пример, чтобы понять евклидово расстояние. Вот оно.
Рис. 3. Евклидово расстояниеЕвклидово расстояние очень похоже на теорему Пифагора.Это наиболее интуитивно понятный тип измерения расстояния, который можно использовать для расчета расстояний между двумя разными точками. Допустим, вы хотите найти расстояние между двумя разными точками в вашем городе, вы можете использовать для этого евклидово расстояние. Вот диаграмма, которая представляет то же самое.
Рис. 3. Евклидово расстояние между двумя разными точкамиВспомните определение смещения в физике. Смещение определяется как кратчайшее расстояние между двумя разными, а также евклидово расстояние.
Манхэттен Дистанция
Если вы хотите найти расстояние Манхэттена между двумя разными точками (x1, y1) и (x2, y2), например, следующим образом, оно будет выглядеть следующим образом:
Манхэттенское расстояние = (x2 — x1) + (y2 — y1)
Схематично это выглядело бы, как если бы вы пересекали путь от точки A до точки B, идя по розовой прямой.
Рис. 4. Манхэттенское расстояние между двумя точками A (x1, y1) и B (x2, y2)Другая диаграмма, которая иллюстрирует манхэттенское расстояние, выглядит следующим образом.Это пройденный путь, обозначенный линией со стрелкой.
Рис. 5 Манхэттенское расстояние между двумя точками A и BДавайте посмотрим на приведенную ниже диаграмму, чтобы понять расстояние Евклида, Манхэттена и Минковского. Обратите внимание, что различное значение P, такое как 1 и 2 в расстоянии Минковского, приводит к Евклидову и Манхэттенскому расстоянию соответственно. Меры расстояния, используемые для измерения расстояния между двумя точками в городе, представлены с различным значением P в формуле расстояния Минковского.
Рис. 6. Расстояние Минковского, Евклидово и Манхэттенское расстояниеКосинусное расстояние / сходство
Косинусное сходство — это мера сходства между двумя ненулевыми векторами. Он вычисляется как внутреннее произведение двух векторов, измеряющее косинус угла между ними. Между наиболее похожими векторами будет 0 градусов. Другими словами, наиболее похожие векторы будут совпадать друг с другом. Значение cos 0 равно 1. Вектор, который будет противоположным друг другу или наиболее непохожим, будет иметь значение -1 (cos (180deg).
Преимущество использования косинусного расстояния заключается в высокой скорости вычисления расстояний между разреженными векторами. Например, если для домов собрано 500 атрибутов, и 200 из них являются взаимоисключающими (это означает, что они есть у одного дома, а у других нет), тогда в расчет нужно будет включить только 300 измерений.
Вот формула косинусного сходства между двумя векторами a и b, имеющими атрибуты в n измерениях
Рис 7.Косинусное сходство между двумя векторамиНа приведенной ниже диаграмме представлено косинусное сходство между двумя векторами, имеющими разный угол между ними.
Рис. 8. Косинусное сходство между двумя векторамиСтатистические измерения расстояний
Статистические меры расстояния используются для расчета расстояния между двумя статистическими объектами. Статистическая мера расстояния используется при решении таких задач, как проверка гипотез, контраст независимости, критерии согласия, задачи классификации, обнаружение выбросов, методы оценки плотности и т. Д.Ниже представлены некоторые из важных типов статистических мер расстояния:
- Расстояние Махаланобиса
- Расстояние Жаккара
Расстояние Махаланобиса
Расстояние Махаланобиса — это один из типов статистической меры расстояния, который используется для вычисления расстояния от точки до центра распределения. Это идеальный вариант для решения проблемы обнаружения выбросов. Расстояние точки P от распределения вероятностей D — это то, насколько далеко стандартное отклонение P находится от среднего значения распределения вероятностей D.Если точка P находится в среднем значении распределения вероятностей, расстояние равно нулю (0).
Может показаться, что две точки имеют одинаковое евклидово расстояние, но разное расстояние Махаланобиса и, следовательно, не похожи. Посмотрите на схему, приведенную ниже.
Рис. 9. Расстояние Махаланобиса (точка X обнаруживается как выброс) — ИсточникВы можете заметить, что точка X может рассматриваться как выброс в распределении данных, показанном на приведенной выше диаграмме, хотя евклидово расстояние красной и зеленой точек то же самое в среднем.
Жаккар Дистанция
Еще один тип статистической меры — Расстояние Жаккара. Учитывает пересечение или перекрытие атрибутов между двумя объектами, между которыми необходимо найти расстояние. Например, допустим, есть две точки, представленные набором атрибутов. Если один или несколько атрибутов для одной точки совпадают с другим, то они будут перекрываться и, следовательно, будут находиться на близком расстоянии. Если бы у точек были разные атрибуты, они бы не совпадали.На следующей диаграмме представлена формула расстояния Жаккара:
Рис. 10. Статистическое измерение расстояния — расстояние Жаккарда Недавно я работал в области науки о данных и машинного обучения / глубокого обучения. Кроме того, я увлечен различными технологиями, включая языки программирования, такие как Java / JEE, Javascript, Python, R, Julia и т. Д., И такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные и т. д.Я хотел бы связаться с вами в Linkedin. Последние сообщения Аджитеша Кумара (посмотреть все) Недавно я работал в области Data Science и Machine Learning / Deep Learning. Кроме того, я увлечен различными технологиями, включая языки программирования, такие как Java / JEE, Javascript, Python, R, Julia и т. Д., И такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные и т. д.Я хотел бы связаться с вами в Linkedin.7 важных мер расстояния в машинном обучении
ВВЕДЕНИЕ:Для таких алгоритмов, как k-ближайший сосед и k-среднее, важно измерить расстояние между точками данных.
В KNN мы вычисляем расстояние между точками, чтобы найти ближайшего соседа, а в K-средних мы находим расстояние между точками, чтобы сгруппировать точки данных в кластеры на основе сходства.
Очень важно выбрать правильную меру расстояния, поскольку она влияет на результаты нашего алгоритма.
В этом посте мы увидим некоторые стандартные меры расстояния, используемые в машинном обучении.
Евклидовое расстояние:Это одна из наиболее часто используемых мер расстояния.
Рассчитывается как квадратный корень из суммы разностей между каждой точкой.
Проще говоря, евклидово расстояние — это длина отрезка прямой, соединяющего точки.
Евклидово расстояние также известно как норма L2 вектора.
def евклидово (x, y): расстояние = 0 для a, b в zip (x, y): расстояние + = (сумма ([(pow ((a-b), 2))])) вернуть sqrt (расстояние) print («Евклидово расстояние:», евклидово ([1,3,4,1], [3,2,1,1]))
def euclidean (x, y): distance = 0 для a, b в zip (x, y): distance + = (sum ([(pow ((ab), 2))]) ) return sqrt (distance) print («Евклидово расстояние:», евклидово ([1,3,4,1], [3,2,1,1])) |
ВЫХОД: Евклидово расстояние: 3.7416573867739413
ВЫХОД: Евклидово расстояние: 3,7416573867739413 |
Также называется расстоянием городского квартала или нормой L1 вектора.
Манхэттенское расстояние рассчитывается как сумма абсолютных расстояний между двумя точками.
def манхэттен (x, y): расстояние = 0 для a, b в zip (x, y): расстояние + = сумма ([абс (а-б)]) расстояние возврата print («Расстояние до Манхэттена:», манхэттен ([1,3,4,1], [3,2,1,1]))
def manhattan (x, y): distance = 0 for a, b in zip (x, y): distance + = sum ([abs (ab)]) return distance print («Манхэттенское расстояние:», манхэттен ([1,3,4,1], [3,2,1,1])) |
ВЫХОД: Манхэттен Расстояние: 6
ВЫХОД: Манхэттен Расстояние: 6 |
Рассчитывается как максимум абсолютной разницы между элементами векторов.
Также называется расстоянием максимального значения.
def chebyshev (x, y): расстояние = [] для a, b в zip (x, y): distance.append (абс (а-б)) печать (расстояние) return max (расстояние) print («Чебышевская дистанция:», чебышев ([1,3,4,1], [3,2,1,1]))
def chebyshev (x, y): distance = [] для a, b в zip (x, y): distance.append (abs (ab)) print (distance) return max (distance) print («Чебышевское расстояние:», chebyshev ([1,3,4,1], [3,2,1,1 ])) |
ВЫХОД: Чебышев Расстояние: 3
ВЫХОД: Чебышев Расстояние: 3 |
Расстояние Минковского — это просто обобщенная форма указанных выше расстояний.
Расстояние Минковского также называется p-нормой вектора.
MINKOWSKI ДЛЯ РАЗНЫХ ЗНАЧЕНИЙ P:Для, p = 1, мера расстояния — это мера Манхэттена.
p = 2, мера расстояния — евклидова мера.
p = ∞, мерой расстояния является мера Чебышева.
ДАЛЬНОСТЬ УБИРАНИЯ:Мы используем расстояние Хэмминга, если нам нужно иметь дело с категориальными атрибутами.
Расстояние Хэмминга определяет, различны ли эти два атрибута или нет.Когда они равны, расстояние равно 0; в противном случае это 1.
Мы можем использовать расстояние Хэмминга, только если струны одинаковой длины.
Например, возьмем две строки «Hello World» и «Hallo Warld».
Расстояние Хэмминга между этими двумя струнами равно 2, поскольку струна различается в двух местах.
def Hamming (x, y): расстояние = 0 для a, b в zip (x, y): если a! = b: расстояние + = 1 расстояние возврата print («Расстояние Хэмминга:», hamming («привет, мир», «привет, варлд»))
def hamming (x, y): distance = 0 for a, b in zip (x, y): if a! = B: distance + = 1 return distance print («Расстояние Хэмминга:», Hamming («привет, мир», «привет, варлд»)) |
ВЫХОД: Расстояние Хэмминга: 2
ВЫХОД: Дистанция Хэмминга: 2 |
Измеряет косинусоидальный угол между двумя векторами.
Косинусное сходство находится в диапазоне от 0 до 1, где 1 означает, что два вектора совершенно похожи.
Если угол между двумя векторами увеличивается, они становятся менее похожими.
Косинусное подобие касается только угла между двумя векторами, а не расстояния между ними.
Предположим, что есть еще один вектор c в направлении b.
Как вы думаете, косинусное сходство будет между b и c?
Косинусное сходство между b и c равно 1, поскольку угол между b и c равен 0, а cos (0) = 1.
Несмотря на то, что расстояние между b и c велико по сравнению с косинусом a и b, сходство касается только направления вектора, а не расстояния.
def cosine_similarity (x, y): числитель = 0 sum_x = 0 sum_y = 0 для a, b в zip (x, y): числитель + = сумма ([a * b]) sum_x + = sum ([a ** 2]) sum_y + = sum ([b ** 2]) знаменатель = округление (sqrt (sum_x) * sqrt (sum_y)) вернуть числитель / знаменатель print («Косинусное подобие:», cosine_similarity ([1,3,4,1], [3,2,1,1]))
def cosine_similarity (x, y): числитель = 0 sum_x = 0 sum_y = 0 для a, b в zip (x, y): числитель + = сумма ([a * b ]) sum_x + = sum ([a ** 2]) sum_y + = sum ([b ** 2]) знаменатель = round (sqrt (sum_x) * sqrt (sum_y)) числитель возврата / знаменатель print («Косинусное сходство:», косинусное сходство ([1,3,4,1], [3,2,1,1])) |
ВЫХОД: Косинусное подобие: 0.7
ВЫХОД: Косинусное сходство: 0,7 |
В подобии Жаккара вместо векторов мы будем использовать множества. Он используется для поиска сходства между двумя наборами.
Сходство Жаккара определяется как пересечение множеств, разделенное их объединением.
Сходство по Жаккару между двумя наборами A и B составляет
. JACCARD РАССТОЯНИЕ:Мы используем расстояние Жаккара, чтобы определить, насколько два набора отличаются друг от друга.
1 — jaccard_similarity даст вам расстояние Жаккарда.
def jaccard_similarity (x, y): пересечение = len (set (x) .intersection (set (y))) union = len (набор (x) .union (набор (y))) возврат (пересечение / объединение) print («Подобие Жаккарда:», jaccard_similarity ([0,1,2,5,6], [0,2,3,4,5,7,9])) print («Расстояние Жаккарда:», 1-jaccard_similarity ([0,1,2,5,6], [0,2,3,4,5,7,9]))
def jaccard_similarity (x, y): пересечение = len (set (x).пересечение (set (y))) union = len (set (x) .union (set (y))) return (пересечение / объединение) print («Подобие Жаккарда:», jaccard_similarity ([0, 1,2,5,6], [0,2,3,4,5,7,9])) print («Расстояние Жаккарда:», 1-jaccard_similarity ([0,1,2,5,6 ], [0,2,3,4,5,7,9])) |
ВЫХОД: Сходство по Жаккару: 0,3333333333333333 Расстояние Жаккарда: 0,6666666666666667
ВЫХОД: Сходство по Жаккару: 0.3333333333333333 Jaccard Расстояние: 0,6666666666666667 |
В этом посте я обсудил различные меры расстояния в машинном обучении. Теперь вопрос в том, какую меру расстояния выбрать?
Вы должны выбрать правильную меру расстояния на основе свойств наших данных.
Евклидово расстояние можно использовать, если входные переменные похожи по типу или если мы хотим найти расстояние между двумя точками.
В случае данных большой размерности манхэттенское расстояние предпочтительнее евклидова.
Расстояние Хэмминга используется для категориальных переменных.
Косинусное подобие можно использовать там, где величина вектора не имеет значения. И Жаккар, и косинусное подобие часто используются при интеллектуальном анализе текста.
Код этого сообщения в блоге можно найти в этом репозитории Github.
Какие существуют типы измерения расстояния?
Евклидово расстояние:
Самая известная мера расстояния — это то, что мы обычно называем «расстоянием».«N-мерное евклидово пространство — это пространство, в котором точки являются векторами n действительных чисел. Условная мера расстояния в этом пространстве, которую мы будем называть L2-нормой, определена:
То есть мы возводим в квадрат расстояние в каждом измерении, суммируем квадраты и извлекаем положительный квадратный корень.
Пример. Рассмотрим двумерное евклидово пространство (обычная плоскость) и точки (2, 7) и (6, 4). L2-норма дает расстояние
L1-норма дает расстояние | 2 — 6 | + | 7 — 4 | = 4 + 3 = 7.L∞-норма дает расстояние
макс. (| 2–6 |, | 7–4 |) = макс (4, 3) = 4
Jaccard Расстояние
Мы определяем расстояние Жаккара множеств как d (x, y) = 1 — SIM (x, y). То есть расстояние Жаккара равно 1 минус отношение размеров пересечения и объединения множеств x и y. Мы должны убедиться, что эта функция является мерой расстояния.
d (x, y) неотрицательно, потому что размер пересечения не может превышать размер объединения.
d (x, y) = 0, если x = y, потому что x ∪ x = x ∩ x = x. Однако, если x 6 = y, то размер x ∩ y строго меньше размера x ∪ y, поэтому d (x, y) строго положительно.
d (x, y) = d (y, x), потому что и объединение, и пересечение симметричны; т.е. x ∪ y = y ∪ x и x ∩ y = y ∩ x.
Косинусное расстояние
Косинусное расстояние имеет смысл в пространствах с размерностями, включая евклидовы пространства и дискретные версии евклидовых пространств, например, в пространствах, где точки являются векторами с целочисленными компонентами или логическими (0 или 1) компонентами.В таком пространстве точки можно рассматривать как направления. Косинусное расстояние между двумя точками — это угол, который образуют векторы к этим точкам. Этот угол будет находиться в диапазоне от 0 до 180 градусов, независимо от того, сколько измерений имеет пространство.
Мы можем вычислить косинусное расстояние, сначала вычислив косинус угла, а затем применив функцию арккосинуса для преобразования в угол в диапазоне 0–180 градусов. Учитывая два вектора x и y, косинус угла между ними является скалярным произведением x.y, деленное на L2-нормы x и y (т.е. их евклидовы расстояния от начала координат).
Изменить расстояние
Это расстояние имеет смысл, когда точки представляют собой струны. Расстояние между двумя строками x = x1x2 • • • xn и y = y1y2 • • • ym — это наименьшее количество вставок и удалений отдельных символов, которые преобразуют x в y.
Расстояние Хэмминга
Учитывая пространство векторов, мы определяем расстояние Хэмминга между двумя векторами как количество компонентов, в которых они различаются.Расстояние Хэмминга не может быть отрицательным, и если оно равно нулю, то векторы идентичны. Расстояние не зависит от того, какой из двух векторов мы рассматриваем в первую очередь. Неравенство треугольника также должно быть очевидным. Если x и z различаются m компонентами, а z и y отличаются n компонентами, то x и y не могут отличаться более чем в m + n компонентах. Чаще всего используется расстояние Хэмминга, когда векторы являются логическими; они состоят только из нулей и единиц. Однако в принципе векторы могут иметь компоненты из любого набора.
Сравнение альтернативных подходов к измерению географической доступности городских служб здравоохранения: типы расстояний и ошибки агрегирования | International Journal of Health Geographics
В недавних исследованиях состояния здоровья в городах повышенное внимание было уделено оценке доступности городских ресурсов как для отдельных лиц, так и для населения, проживающего в жилых районах. Хотя концепция «доступности» многомерна (доступность может быть определена с точки зрения доступности, приемлемости, наличия и пространственной доступности [1]), оценка географической доступности в жилых районах предлагает важную информацию для государственной политики при планировании и предоставлении услуг, поскольку она позволяет: выявление территорий с более низким (или более высоким) доступом к городским ресурсам и оценка пространственного и социального неравенства в доступе [2, 3].
Географическая доступность означает легкость, с которой жители данной области могут получить доступ к услугам и объектам [2]. Наиболее распространенные подходы к определению географической доступности основаны на расстоянии или времени в пути до ресурса (для обзора см. [4]). Эти меры предполагают, что каждый член населения является потенциальным пользователем услуги; модель пространственной доступности будет зависеть от относительного расположения населения и услуг [5, 6]. В таблице 1 обобщены подходы к концептуализации и измерению различных аспектов географической доступности.
Таблица 1 Подходы к концептуализации и измерению географической доступности услуг и объектов для жилых районовВ нескольких исследованиях измерялась географическая доступность в жилых районах услуг и объектов, которые могут способствовать благосостоянию и здоровью населения, например как службы здравоохранения [2, 7–18], места отдыха [2, 16, 18, 19] и продуктовые супермаркеты [16, 18, 20–23]. Доступность этих типов ресурсов особенно важна для групп населения с ограниченной мобильностью и доходами, поскольку более прямой и легкий доступ открывает возможности за счет сокращения временных и финансовых затрат на доступ и потенциально влияет на выбор жизни [24].В других исследованиях измерялась географическая доступность ресурсов, потенциально связанных с более негативными последствиями для здоровья, таких как мусоропроводы, рестораны быстрого питания и загрязнение от крупных автомагистралей [25–27].
За последние два десятилетия применение показателей географической доступности в исследованиях городов и здоровья стало проще, во многом благодаря развитию программного обеспечения и модулей ГИС для транспортировки. Эти меры требуют определения набора из четырех параметров, а именно: 1) пространственная эталонная единица для населения, т.е.е. определение жилых районов; 2) метод агрегирования, т. Е. Для учета распределения населения в жилой зоне; 3) мера доступности; и 4) тип расстояния для вычисления выбранных мер доступности. Выбор этих параметров может привести к различным результатам, что может привести к значительным ошибкам измерения [2, 28, 29].
В этой статье мы исследуем различия в результатах, когда географическая доступность жилых районов (участков переписи) для медицинских услуг рассчитывается с использованием различных типов расстояний и различных методов агрегирования.В следующем разделе мы описываем методы определения четырех параметров для вычисления показателей доступности. Помня об этих методах, мы затем даем обзор методологических проблем измерения доступности.
Оценка географической доступности услуг и объектов в жилых районах: определение набора параметров
Пространственная единица отсчета и методы агрегирования
Выбор соответствующей пространственной единицы анализа, то есть рабочего определения для жилых районов, имеет решающее значение для минимизации агрегирования ошибки [2, 30].Ошибка агрегирования возникает из-за распределения особей вокруг центроида пространственных единиц [2]. Поскольку пространственные единицы различаются по размеру от небольших участков, например переписные участки, на более крупные, например переписных участков, доступность, измеренная для небольших единиц, меньше подвержена ошибкам агрегирования, чем доступность, измеренная для более крупных пространственных единиц [2].
Для оценки географической доступности услуги для населения, проживающего в жилом районе, например переписной участок, можно использовать три метода [2]; они показаны на рисунке 1.Первый метод заключается в вычислении расстояния между центром тяжести переписного участка и услугой (рис. 1.a). Этот метод показывает нецелесообразность игнорирования пространственного распределения населения внутри переписного участка [2].
Рисунок 1Выбор пространственной единицы отсчета для вычисления расстояний и агрегирования ошибок.
Второй метод состоит из расчета средневзвешенного по численности населения центра участков переписи (уравнение 1), а затем оценки расстояния между этим новым местоположением и услугой.С этой целью могут использоваться более мелкие пространственные единицы, полностью содержащиеся в переписных участках, такие как районы распространения, участки переписи или почтовые индексы. Этот метод учитывает пространственное распределение населения внутри переписного участка, чтобы минимизировать ошибку агрегирования.
(Xi, Yi) = (Σb∈iwbxbΣb∈iwb, Σk∈iwbybΣb∈iwb) MathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = @ 63D3 @(1)
Где:
w b = общая численность населения территориальной единицы b полностью в пределах переписного участка i (т.е. область распространения, или блок переписи, или почтовый индекс).
x b и y b = X и Y координаты пространственной единицы b .
Наконец, третий метод заключается в вычислении расстояния между услугами и каждым центроидом пространственных единиц полностью в пределах переписных участков, а затем вычислении среднего значения этих расстояний, взвешенных по общей численности населения каждой единицы (рис.б и 1в). По сравнению с предыдущими методами, этот более точен, потому что он более точно учитывает распределение населения внутри переписного участка.
Показатели доступности
Пять наиболее часто используемых показателей доступности: 1) расстояние до ближайшего сервиса, 2) количество сервисов в пределах n метров или минут, 3) среднее расстояние до всех сервисов, 4) среднее расстояние до n ближайших сервисов и 5) гравитационная модель.Если более точный метод агрегации подробно ранее выбран, эти меры доступности можно записать в виде:
Зиа = Σb∈iwb (мин | DBS |) Σb∈iwb, MathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdggaHbaakiabg2da9KqbaoaalaaabaWaaabuaeaacqWG3bWDdaWgaaqaaiabdkgaIbqabaGaeiikaGIagiyBa0MaeiyAaKMaeiOBa42aaqWaaeaacqWGKbazdaWgaaqaaiabdkgaIjabdohaZbqabaaacaGLhWUaayjcSdGaeiykaKcabaGaemOyaiMaeyicI4SaemyAaKgabeGaeyyeIuoaaeaadaaeqbqaaiabdEha3naaBaaabaGaemOyaigabeaaaeaacqWGIbGycqGHiiIZcqWGPbqAaeqacqGHris5aaaakiabcYcaSaaa @ 5225 @(2)
Где:
ZiaMathType @ СПР @ 5 @ 5 @ + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdggaHbaaaaa @ 2FE3 @ = среднее расстояние между переписным трактом я и ближайшим сервисом.
w b = общая численность населения территориальной единицы b полностью в пределах переписного участка i .
d bs = расстояние между пространственной единицей b и службой s .
Zib = Σb∈iWbΣj∈SSjΣb∈iWb, MathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaacbmGae8NwaO1aa0baaSqaaiabdMgaPbqaaiabdkgaIbaakiabg2da9maalaaabaWaaabuaeaacqWFxbWvdaWgaaWcbaGaemOyaigabeaaaeaacqWGIbGycqGHiiIZcqWGPbqAaeqaniabggHiLdGcdaaeqbqaaiab = nfatnaaBaaaleaacqWGQbGAaeqaaaqaaiabdQgaQjabgIGiolabdofatbqab0GaeyyeIuoaaOqaamaaqafabaGae83vaC1aaSbaaSqaaiabdkgaIbqabaaabaGaemOyaiMaeyicI4SaemyAaKgabeqdcqGHris5aaaakiabcYcaSaaa @ 4D15 @(3)
Где:
ZibMathType @ СПР @ 5 @ 5 @ + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdkgaIbaaaaa @ 2FE5 @ = среднее число услуг в пределах п метров или минут переписи тракта я .
w b = общая численность населения территориальной единицы b полностью в пределах переписного участка i .
S = все услуги.
S J = количество услуг в пределах n метров или минут центроида пространственной единицы b с S j = 1, где d bs ≤ n и S j = 0, где d bs > n .
Зик = Σb∈iwbdbsΣb∈iwb, MathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdogaJbaakiabg2da9KqbaoaalaaabaWaaabuaeaacqWG3bWDdaWgaaqaaiabdkgaIbqabaGaemizaq2aaSbaaeaacqWGIbGycqWGZbWCaeqaaaqaaiabdkgaIjabgIGiolabdMgaPbqabiabggHiLdaabaWaaabuaeaacqWG3bWDdaWgaaqaaiabdkgaIbqabaaabaGaemOyaiMaeyicI4SaemyAaKgabeGaeyyeIuoaaaGccqGGSaalaaa @ 4933 @(4)
ZicMathType @ СПР @ 5 @ 5 @ + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdogaJbaaaaa @ 2FE7 @ = среднее расстояние между переписной тракта я населения и все услуги.
w b = общая численность населения территориальной единицы b полностью в пределах переписного участка i .
d bs = расстояние между центроидом пространственной единицы b и службой s .
Zid = Σb∈iwbΣsdbsnΣb∈iwb, MathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdsgaKbaakiabg2da9KqbaoaalaaabaWaaabuaeaacqWG3bWDdaWgaaqaaiabdkgaIbqabaWaaabuaeaadaWcaaqaaiabdsgaKnaaBaaabaGaemOyaiMaem4CamhabeaaaeaacqWGUbGBaaaabaGaem4CamhabeGaeyyeIuoaaeaacqWGIbGycqGHiiIZcqWGPbqAaeqacqGHris5aaqaamaaqafabaGaem4DaC3aaSbaaeaacqWGIbGyaeqaaaqaaiabdkgaIjabgIGiolabdMgaPbqabiabggHiLdaaaOGaeiilaWcaaa @ 4E24 @(5)
ZidMathType @ СПР @ 5 @ 5 @ + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdsgaKbaaaaa @ 2FE9 @ = среднее расстояние между переписным трактом я и п ближайшими услугами.
w b = общая численность населения территориальной единицы b полностью в пределах переписного участка i .
d bs = расстояние между центроидом пространственной единицы b и службой s, d bs отсортирован по возрастанию.
n = количество ближайших услуг, которые должны быть включены в показатель.
Zie = Σb∈iwbΣSSwsdbs-αΣb∈iwb, MathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdwgaLbaakiabg2da9KqbaoaalaaabaWaaabuaeaacqWG3bWDdaWgaaqaaiabdkgaIbqabaWaaabuaeaacqWGtbWudaWgaaqaaiabdEha3jabdohaZbqabaGaemizaq2aa0baaeaacqWGIbGycqWGZbWCaeaacqGHsisliiGacqWFXoqyaaaabaGaem4uamfabeGaeyyeIuoaaeaacqWGIbGycqGHiiIZcqWGPbqAaeqacqGHris5aaqaamaaqafabaGaem4DaC3aaSbaaeaacqWGIbGyaeqaaaqaaiabdkgaIjabgIGiolabdMgaPbqabiabggHiLdaaaOGaeiilaWcaaa @ 533B @(6)
ZieMathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xH8viVGI8Gi = hEeeu0xXdbba9frFj0xb9qqpG0dXdb9aspeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemOwaO1aa0baaSqaaiabdMgaPbqaaiabdwgaLbaaaaa @ 2FEB @ = среднее значение потенциальной силы тяжести.
w b = общая численность населения территориальной единицы b полностью в пределах переписного участка i .
S = количество услуг в исследуемой области.
d bs = расстояние между центроидом пространственной единицы b и службой s .
α = параметр трения (обычно 1, 1,5 или 2).
S WS = вес, присвоенный услуге s , такой как ее размер (например, количество коек в больнице).
Типы расстояний
Для расчета показателей доступности обычно используются четыре типа расстояний: Евклидово расстояние (прямолинейное), Манхэттенское расстояние (расстояние по двум сторонам прямоугольного треугольника, противоположное гипотенузе), кратчайшее сетевое расстояние и кратчайшее сетевое время (рисунок 2) [28, 31]. Расстояние Евклида и Манхэттена можно легко вычислить с использованием географических координат:
Рисунок 2Несколько видов дистанции.
Dij = (хи-Xj) 2+ (у-YJ) 2, MathType @ СПР @ 5 @ 5 + = feaafiart1ev1aaatCvAUfKttLearuWrP9MDH5MBPbIqV92AaeXatLxBI9gBaebbnrfifHhDYfgasaacPC6xNi = xI8qiVKYPFjYdHaVhbbf9v8qqaqFr0xc9vqFj0dXdbba91qpepeI8k8fiI + FSY = rqGqVepae9pg0db9vqaiVgFr0xfr = XFR = xc9adbaqaaeGacaGaaiaabeqaaeqabiWaaaGcbaGaemizaq2aaSbaaSqaaiabdMgaPjabdQgaQbqabaGccqGH9aqpdaGcaaqaaiabcIcaOiabdIha4naaBaaaleaacqWGPbqAaeqaaOGaeyOeI0IaemiEaG3aaSbaaSqaaiabdQgaQbqabaGccqGGPaqkdaahaaWcbeqaaiabikdaYaaakiabgUcaRiabcIcaOiabdMha5naaBaaaleaacqWGPbqAaeqaaOGaeyOeI0IaemyEaK3aaSbaaSqaaiabdQgaQbqabaGccqGGPaqkdaahaaWcbeqaaiabikdaYaaaaeqaaOGaeiilaWcaaa @ 46F8 @(7)
д ij = | x i — x j | + | и и — год год |,
Где:
X i и Y i = Координаты X и Y точки i с проекцией на плоскость.
С другой стороны, расчет сетевого расстояния и сетевого временного расстояния, которые представляют соответственно кратчайший и самый быстрый пути между двумя точками с использованием уличной сети, является более сложным. Действительно, для вычисления этих двух расстояний требуются файлы геометрической сети — с указаниями, ограничениями скорости, ограничениями поворотов и задержками, доступными для каждого сегмента улицы, — интегрированные в ГИС, а также модуль ГИС или программное обеспечение ГИС, специализирующееся на анализе транспорта (расширение ESRI Network Analyst Extension или программное обеспечение TransCad, например).
Кратчайшие сетевые и сетевые временные расстояния представляют две разные цели. Кратчайшее сетевое расстояние полезно для оценки пути между двумя точками, как если бы он шел пешком; следовательно, он часто используется в исследованиях доступности «ближайших» услуг и сооружений [4, 18, 20, 32–34]. Кратчайшее расстояние по времени является более точным для оценки расстояний на машине или общественном транспорте.
Методологические вопросы и точность измерения географической доступности
При оценке географической доступности выбор этих параметров может дать разные результаты, что может привести к значительным ошибкам измерения [2, 28, 29].
Большинство исследований, изучающих географическую доступность здравоохранения и связанных со здоровьем услуг, были связаны с измерением доступности ближайшего медицинского учреждения с использованием евклидова расстояния [2, 13], кратчайшего сетевого расстояния [8, 18, 32], кратчайшего сетевого времени. distance [9, 11, 16, 17, 35] или комбинация типов расстояния [10, 12, 15]. Другие также исследовали близость к разнообразию, измеряя среднее кратчайшее сетевое расстояние до выбранных услуг [32], и предложение, предоставляемое ближайшим окружением, т.е.е. количества услуг на заданном расстоянии [7, 14, 18, 32]. Несколько исследований концептуализировали различные аспекты географической доступности в рамках одного исследования (исключения см. [14, 15, 32]), хотя это было бы полезно для описания сложности географической доступности данной услуги [32]. Более того, в пределах данного набора данных выбор меры доступности является фундаментальным, поскольку доступность варьируется в зависимости от используемого показателя [3, 4, 36].
В некоторых исследованиях сравнивались расхождения в результатах, когда географическая доступность измерялась с использованием разных типов расстояний. В исследовании, посвященном поиску компромиссов между различными типами расстояний, Аппарисио и его коллеги [28] сравнили матрицы расстояний, основанные на простых (евклидовом, манхэттенском) и сетевом (дорога, время) измерениях расстояния между всеми переписными участками в восьми крупнейших мегаполисах Канады. . Они исследовали, коррелируют ли приближения Евклида и Манхэттена с более точной мерой расстояния, т.е.е. время в пути по сети дорог, на уровне метрополии и переписных участков. Авторы пришли к выводу, что на уровне мегаполисов использование евклидовых или манхэттенских расстояний для оценки кратчайшего сетевого времени не вносит серьезных ошибок. Однако в пригородах или районах, расположенных вдали от центрального делового района, использование евклидовой или манхэттенской аппроксимации кратчайшего сетевого времени может привести к существенным ошибкам. При измерении доступности в этих областях сетевые матрицы расстояния / времени могут дать более подходящие результаты.Аналогичные результаты наблюдались также [10, 12, 15].
Что касается рабочего определения жилых районов, использовалось большое количество единиц площади, начиная от более мелких единиц, таких как сетчатые блоки переписи [9, 10, 16, 18], счетные участки [11, 13] и районы результатов переписи. [12] в более крупные единицы, такие как переписные участки [7, 17, 32, 35], общины и определенные городами кварталы [2, 8] и районы [13–15]. Некоторые исследования контролировали расположение населения в пространственной единице, вычисляя средневзвешенный центр пространственной единицы [12, 14, 16, 17, 35] или вычисляя средневзвешенную для населения доступность более мелких пространственных единиц. находится в интересующей пространственной единице [2, 13, 32].Тем не менее, в значительном количестве исследований не используются методы минимизации ошибок агрегирования, т.е. в них вычисляется доступность геометрического центроида пространственной единицы.
Для государственной политики и планирования измерение географической доступности городских ресурсов и объектов представляет интерес, поскольку оно дает информацию о наличии благоприятных ресурсов [37] или структур возможностей [38] в жилой среде. Однако меры географической доступности подвержены множеству методологических проблем, среди которых есть ошибки, вызванные использованием различных типов расстояний [28] и методов агрегирования [2, 29].
Цели исследования
В этой статье мы исследуем различия в результатах, когда географическая доступность жилых районов (участков переписи) для выбранных медицинских услуг рассчитывается с использованием различных типов расстояний и различных методов агрегирования. Конкретные цели заключаются в следующем: 1) Сравнить меры расстояний; и 2) Оценить ошибки агрегирования для нескольких показателей доступности.
